BST(이진탐색트리) 구현
종료(q) 명령 때까지 삽입(i), 탐색(s), 삭제(d), 인쇄(p), 명령을 반복 입력받아 수행
i <키>: 입력 <키>에 대한 노드 생성 및 트리에 삽입
d <키>: 입력 <키>가 트리에 존재하면 해당 노드 삭제 후 삭제된 키를 출력, 없으면 ‘X’를 출력
s <키>: 입력 <키>가 트리에 존재하면 해당 키를 출력, 없으면 ‘X’를 출력
p: 현재 트리를 전위순회로 인쇄
q: 프로그램 종료
주의:
- 중복 키가 없는 것으로 전제한다.
- 문제를 단순화하기 위해, 키만 존재하고 원소(element)는 없는 것으로 구현한다.
- main 함수는 반복적으로 명령을 입력받기 전에 빈(empty) 이진탐색트리를 초기화해야 한다 – 즉, 외부노드 1개로만 구성된 이진트리를 말한다.
힌트:
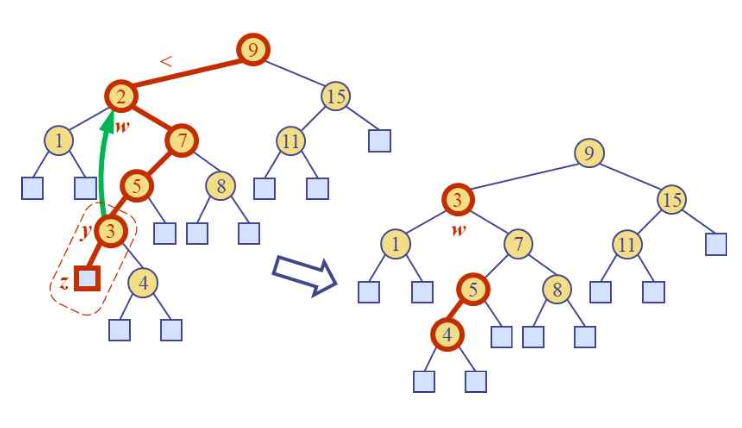
- 트리 노드 삭제 시, 삭제할 노드 w의 자식 중 하나(z이라 하자)라도 잎인 경우는 아래 그림 <삭제 예시 1>처럼 w를 z과 함께 삭제하고, 반대쪽 자식 노드(그림에서 8을 저장한 노드)가 w를 계승한다 – reduceExternal(z) 함수 사용.

2. 삭제할 노드 w의 자식 둘 다 내부 노드인 경우는 w의 중위순회 후계자 y가 삭제한 노드 위치에 오도록 한다. 중위순회 후계자를 찾는 방법은 오른쪽 자식으로 이동한 후, 거기서부터 왼쪽 자식들만을 끝까지 따라 내려가서 도달하게 되는 내부노드를 찾는 것이다(그림 <삭제 예시 2> 참고).





(전체코드)
// 문제를 단순화하기 위해, 키만 존재하고 원소를 키라 가정
// 외부노드는 실제 키를 가지고 있지 않고, 새로운 노드를 삽입할 위치를 나타내는 역할이다
#include <stdio.h>
#include <stdlib.h>
typedef struct NODE {
int key;
struct NODE* parent;
struct NODE* lChild;
struct NODE* rChild;
} NODE;
NODE* g_root = NULL;
// 기본 메서드
int isExternal(NODE* node);
NODE* createEmptyNode();
NODE* getSibling(NODE* node);
NODE* inorderSucc(NODE* node); // 중위순회 계승자를 반환하는 함수
void printPreorder(NODE* node);
void freeNode(NODE* node);
// 로직 함수들
NODE* treeSearch(int k); // 트리에서 키를 저장한 내부 노드를 반환하는 함수, 혹은 그런 노드가 없다면 삽입될 위치의 외부 노드를 반환
int getKey(int k);
void insertKey(int k); // 외부노드에 키값을 삽입하는 함수
NODE* expandExternal(NODE* node); // 외부노드를 추가해주는 함수
int deleteKey(int k);
void reduceExternal(NODE* externalNode); // 외부 노드를 제거하고 트리를 재구성하는 함수
int main() {
char cmd;
int key;
int res;
// 초기화: 외부 노드만 있는 빈 트리 생성
g_root = createEmptyNode();
while (1) {
scanf(" %c", &cmd);
if (cmd == 'i') { // insert
scanf(" %d", &key);
insertKey(key);
}
else if (cmd == 'd') { // delete
scanf(" %d", &key);
res = deleteKey(key);
if (res == -1)
printf("X\n"); // 키가 존재하지 않으면 X 출력
else
printf("%d\n", res);
}
else if (cmd == 's') { // search
scanf(" %d", &key);
res = getKey(key);
if (res == -1)
printf("X\n"); // 키가 존재하지 않으면 X 출력
else
printf("%d\n", res);
}
else if (cmd == 'p') { // print
printPreorder(g_root);
printf("\n");
}
else if (cmd == 'q') { // quit
break;
}
}
return 0;
}
int isExternal(NODE* node) {
return node->lChild == NULL && node->rChild == NULL;
}
NODE* createEmptyNode() {
NODE* node = (NODE*)malloc(1 * sizeof(NODE));
node->parent = NULL;
node->lChild = NULL;
node->rChild = NULL;
return node;
}
NODE* getSibling(NODE* node) {
if (node->parent->lChild == node) return node->parent->rChild;
else return node->parent->lChild;
}
// 중위순회 계승자를 반환하는 함수
NODE* inorderSucc(NODE* node) {
NODE* nextNode = node->rChild;
if (isExternal(nextNode)) return NULL;
while (!isExternal(nextNode->lChild)) {
nextNode = nextNode->lChild;
}
return nextNode;
}
void printPreorder(NODE* node) {
if (isExternal(node)) return;
printf(" %d", node->key); // 노드 출력
printPreorder(node->lChild); // 왼쪽 자식으로 이동
printPreorder(node->rChild); // 오른쪽 자식으로 이동
}
void freeNode(NODE* node) {
if (isExternal(node)) return;
freeNode(node->lChild);
freeNode(node->rChild);
free(node);
}
// 트리에서 키를 저장한 내부 노드를 반환하는 함수, 혹은 그런 노드가 없다면 삽입될 위치의 외부 노드를 반환
NODE* treeSearch(int k) {
NODE* node = g_root;
while (!isExternal(node)) {
if (k == node->key) return node; // 키를 찾으면 노드 반환
else if (k < node->key) node = node->lChild; // 키가 작으면 왼쪽으로 이동
else node = node->rChild; // 키가 크면 오른쪽으로 이동
}
return node; // 삽입될 위치의 외부 노드 반환
}
int getKey(int k) {
NODE* targetNode = treeSearch(k);
if (isExternal(targetNode)) {
return -1;
}
return targetNode->key;
}
// 외부노드에 키값을 삽입하는 함수
void insertKey(int k) {
NODE* targetNode = treeSearch(k);
if (isExternal(targetNode)) {
targetNode->key = k;
targetNode = expandExternal(targetNode);
}
}
// 외부노드를 추가해주는 함수
// 외부 노드는 삽입될 위치를 나타내며, 실제로 키가 존재하지 않는 상태
NODE* expandExternal(NODE* node) {
NODE* leftChild = createEmptyNode();
NODE* rightChild = createEmptyNode();
node->lChild = leftChild;
leftChild->parent = node;
node->rChild = rightChild;
rightChild->parent = node;
return node;
}
int deleteKey(int k) {
NODE* node = treeSearch(k);
if (isExternal(node)) return -1; // 삭제할 노드가 존재 x (외부노드는 실제 키를 가지고 있지 않고, 새로운 노드를 삽입할 위치를 나타내는 역할이다)
NODE* nodeToDelete;
if (isExternal(node->lChild)) // 왼쪽 자식이 외부 노드인 경우
nodeToDelete = node->lChild;
else if (isExternal(node->rChild)) // 오른쪽 자식이 외부 노드인 경우
nodeToDelete = node->rChild;
else { // 두 자식이 모두 내부 노드인 경우
NODE* succNode = inorderSucc(node);
node->key = succNode->key; // 중위 순회 후계자의 키를 복사
nodeToDelete = succNode->lChild; // succNode의 왼쪽 자식을 nodeToDelete로 설정
}
reduceExternal(nodeToDelete); // 외부 노드를 제거하고 트리를 재구성
return k;
}
// 외부 노드를 제거하고 트리를 재구성하는 함수
void reduceExternal(NODE* externalNode) {
NODE* parentNode = externalNode->parent;
NODE* siblingNode = getSibling(externalNode);
if (parentNode == g_root) {
g_root = siblingNode;
siblingNode->parent = NULL;
}
else {
NODE* grandparentNode = parentNode->parent;
siblingNode->parent = grandparentNode;
if (parentNode == grandparentNode->lChild)
grandparentNode->lChild = siblingNode; // parentNode가 왼쪽 자식인 경우
else
grandparentNode->rChild = siblingNode; // parentNode가 오른쪽 자식인 경우
}
free(externalNode);
free(parentNode);
}
/*
i 9
i 2
i 15
i 1
i 7
i 11
i 5
i 8
i 3
i 4
p
*/
출처 및 참고: 알고리즘-원리와 응용(국형준교수님), Algorithm Design(Jon Kleinberg, Eva Tardos), Foundations of Algorithms using C++(Richard Neapolitan)
'Computer Science > 알고리즘' 카테고리의 다른 글
| [알고리즘] ep4) 해시테이블(hashtable) (0) | 2024.07.18 |
|---|---|
| [알고리즘] ep3++) AVL 트리 구현 (0) | 2024.07.17 |
| [알고리즘] ep3) 탐색트리 (0) | 2024.07.11 |
| [알고리즘] ep2) 사전(dictionary) (0) | 2024.07.11 |
| [알고리즘] ep1-6+) 퀵정렬의 다양한 버전 (0) | 2024.07.10 |



