ㅇ이진탐색트리(BST, Binary Search Tree): 노드의 왼쪽 가지에는 노드보다 작은 값들만 있고, 노드의 오른쪽 가지에는 노드보다 큰 값들만 있도록 구성

내부노드에 (key, value)쌍을 저장하며 그림으로는 간단히 노드에 key만 표시한다
(왼쪽 및 오른쪽 부트리 또한 각각 이진탐색트리이다)
<재귀 버전>
// 재귀버전
int binarySearch(int* arr, int lowIdx, int highIdx, int key) {
if (lowIdx > highIdx) {
if (highIdx < 0) return -1; // 찾고자 하는 값보다 작은 값이 없는 경우
return highIdx; // 가장 가까운 작은 값의 인덱스를 반환
}
int midIdx = lowIdx + (highIdx - lowIdx) / 2;
if (arr[midIdx] > key) { // 중간값이 키값보다 큰 경우, 왼쪽 절반을 탐색
return binarySearch(arr, lowIdx, midIdx - 1, key);
} else if (arr[midIdx] < key) { // 중간값이 키값보다 작은 경우, 오른쪽 절반을 탐색
return binarySearch(arr, midIdx + 1, highIdx, key);
} else if (arr[midIdx] == key) {
return midIdx;
}
}
<반복문 버전>
// 반복문 버전
int binarySearch(int* arr, int n, int key) {
int lowIdx = 0;
int highIdx = n - 1;
while (lowIdx <= highIdx) {
int midIdx = lowIdx + (highIdx - lowIdx) / 2;
if (arr[midIdx] > key) { // 중간값이 키값보다 큰 경우, 왼쪽 절반을 탐색
highIdx = midIdx - 1;
} else if (arr[midIdx] < key) { // 중간값이 키값보다 작은 경우, 오른쪽 절반을 탐색
lowIdx = midIdx + 1;
} else if (arr[midIdx] == key) { // 중간값과 키값이 일치하는 경우 종료
return midIdx;
}
}
return -1;
}
평균 / 최선: O(log n) - 이진탐색

최악: O(n) - 트리가 한쪽으로 치우친 경우
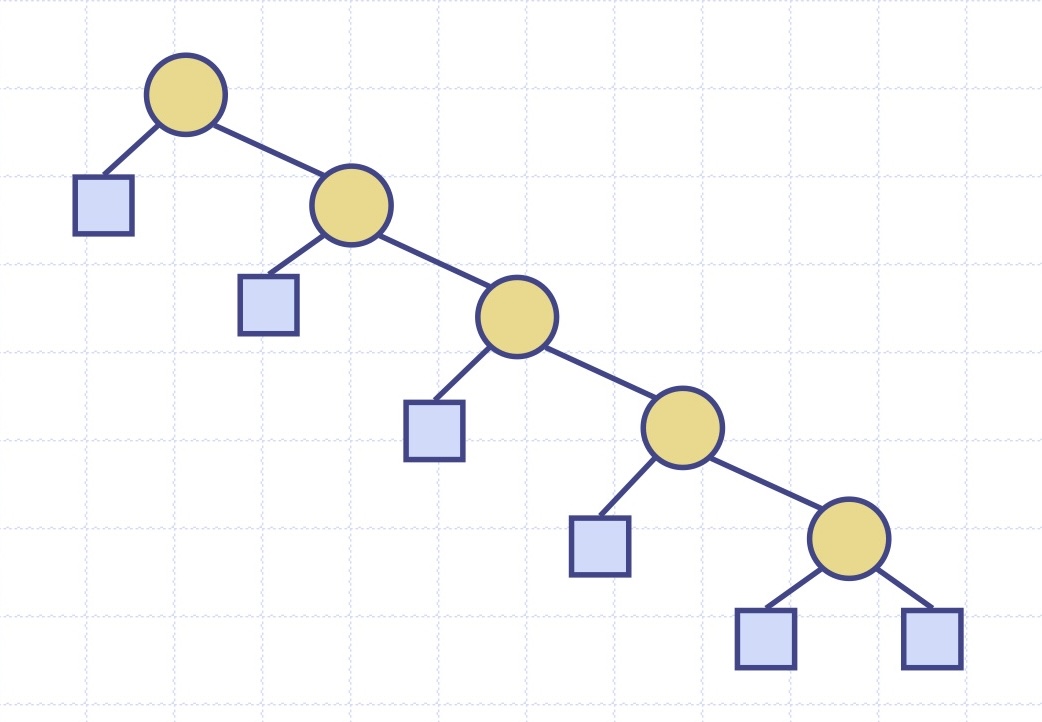
이러한 최악의 O(n) 시간복잡도가 생기는 경우를 막기 위해 나온 것이 자가 균형 이진탐색트리이다
ㅁ자가 균형 이진탐색트리(Self-Balancing Binary Search Tree): 트리가 항상 균형을 유지하도록 하여 최악의 경우에도 O(log n)의 시간복잡도를 보장한다
ㅇAVL 트리: 모든 노드의 왼쪽 서브트리와 오른쪽 서브트리의 높이 차이가 최대 1인 트리
※ AVL(Adelson-Velsky and Landis)은 발명자 이름 약자이다
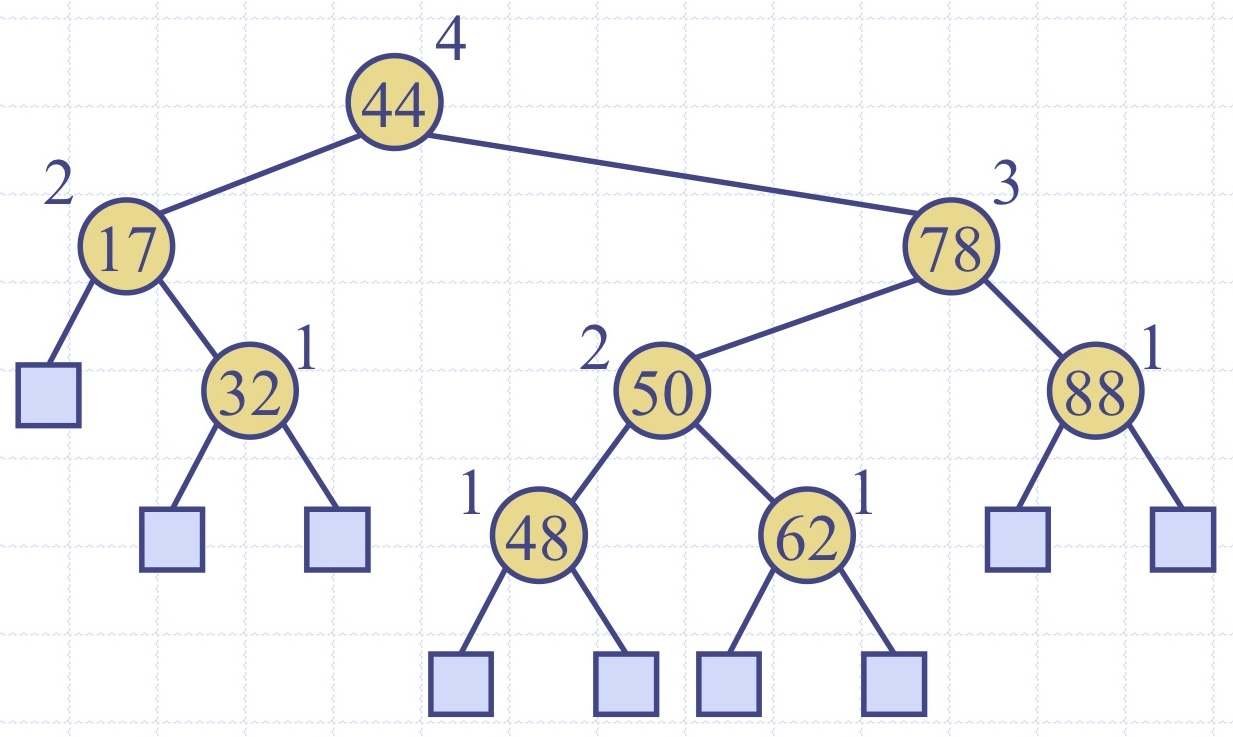
각 노드의 BF는 -1, 0, 1 중 하나의 값을 가진다
- BF가 0이면, 해당 노드의 왼쪽 서브트리와 오른쪽 서브트리의 높이가 같다
- BF가 1이면, 왼쪽 서브트리가 오른쪽 서브트리보다 한 단계 더 높다
- BF가 -1이면, 오른쪽 서브트리가 왼쪽 서브트리보다 한 단계 더 높다
따라서 깨진 균형을 맞추기 위해 삽입/삭제를 할 때마다 트리의 일부를 왼쪽 혹은 오른쪽으로 회전(rotate)시킨다
[AVL 트리의 회전 연산(rotation) 네 가지]
단일 회전(Single Rotation)
- LL 회전: 왼쪽 자식의 왼쪽 부트리로 인해 불균형이 발생한 경우
불균형이 일어난 노드를 기준으로 오른쪽으로 회전

- RR 회전: 오른쪽 자식의 오른쪽 부트리로 인해 불균형이 발생한 경우
불균형이 일어난 노드를 기준으로 왼쪽으로 회전

이중 회전(Double Rotation)
- LR 회전: 왼쪽 자식의 오른쪽 부트리로 인해 불균형이 발생한 경우
왼쪽 자식에 대해 왼쪽 회전(RR)을 하고, 전체 트리에 대해 오른쪽 회전(LL)

- RL 회전: 오른쪽 자식의 왼쪽 부트리로 인해 불균형이 발생한 경우
오른쪽 자식에 대해 오른쪽 회전(LL)을 하고, 전체 트리에 대해 왼쪽 회전(RR)

ㅇ스플레이 트리(Splay Tree): 빈번하게 접근되는 요소들이 더 빠르게 접근될 수 있도록 재구성하는 트리
스플레이(splay) 연산을 통해 트리를 균형 상태로 유지한다
[스플레이 상황]

[스플레이 트리의 회전 연산(rotation) 세 가지]
1. Zig 회전: 노드가 루트의 자식일 때 사용

2. Zig-Zig 회전: 노드와 그 부모 노드가 모두 같은 방향(왼쪽 또는 오른쪽)의 자식일 때 사용

3. Zig-Zag 회전: 노드와 그 부모 노드가 서로 다른 방향의 자식일 때 사용

[스플레이 과정 예시]
3가지 모두 스플레이가 일어날 수 있는 상황이다
① 키 14에 대한 성공적인 탐색 or 키 15에 대한 실패한 탐색
② 키 14을 삽입
③ 키 14를 저장한 노드의 자식노드를 삭제




ㅇ레드-블랙 트리: 노드가 블랙 또는 레드의 색깔을 갖는 트리
- 루트 노드는 항상 블랙 노드
- 레드 노드의 자식은 블랙 노드 (두 개의 연속된 레드 노드 x)
- 모든 리프 노드(더미 노드)는 블랙
- 삽입과 삭제 시 경우에 따라 노드의 색 변환 또는 트리 회전(rotate)이 필요
구현은 꽤나 복잡하지만 실 사용에선 매우 효율적인 모습을 보인다
ㅇ2-3 트리: 각 노드가 2개 또는 3개의 자식을 가질 수 있는 트리
"모든 리프 노드가 동일한 깊이에 위치"
ㅇ2-3-4 트리: 각 노드가 2개 또는 3개 또는 4개의 자식을 가질 수 있는 트리
"모든 리프 노드가 동일한 깊이에 위치"
(B트리와 매우 유사하다)
ㅇB트리: 다방향 트리로, 각 노드가 여러 개의 자식을 가질 수 있다
"모든 리프 노드가 동일한 깊이에 위치"
(DB or 파일 시스템에서 많이 사용된다)
출처 및 참고: 알고리즘-원리와 응용(국형준교수님), Algorithm Design(Jon Kleinberg, Eva Tardos), Foundations of Algorithms using C++(Richard Neapolitan)
'Computer Science > 알고리즘' 카테고리의 다른 글
| [알고리즘] ep3++) AVL 트리 구현 (0) | 2024.07.17 |
|---|---|
| [알고리즘] ep3+) 이진탐색트리(BST) 구현 (0) | 2024.07.17 |
| [알고리즘] ep2) 사전(dictionary) (0) | 2024.07.11 |
| [알고리즘] ep1-6+) 퀵정렬의 다양한 버전 (0) | 2024.07.10 |
| [알고리즘] ep1-4+) O(n + klog(n))의 힙정렬 (0) | 2024.07.10 |


