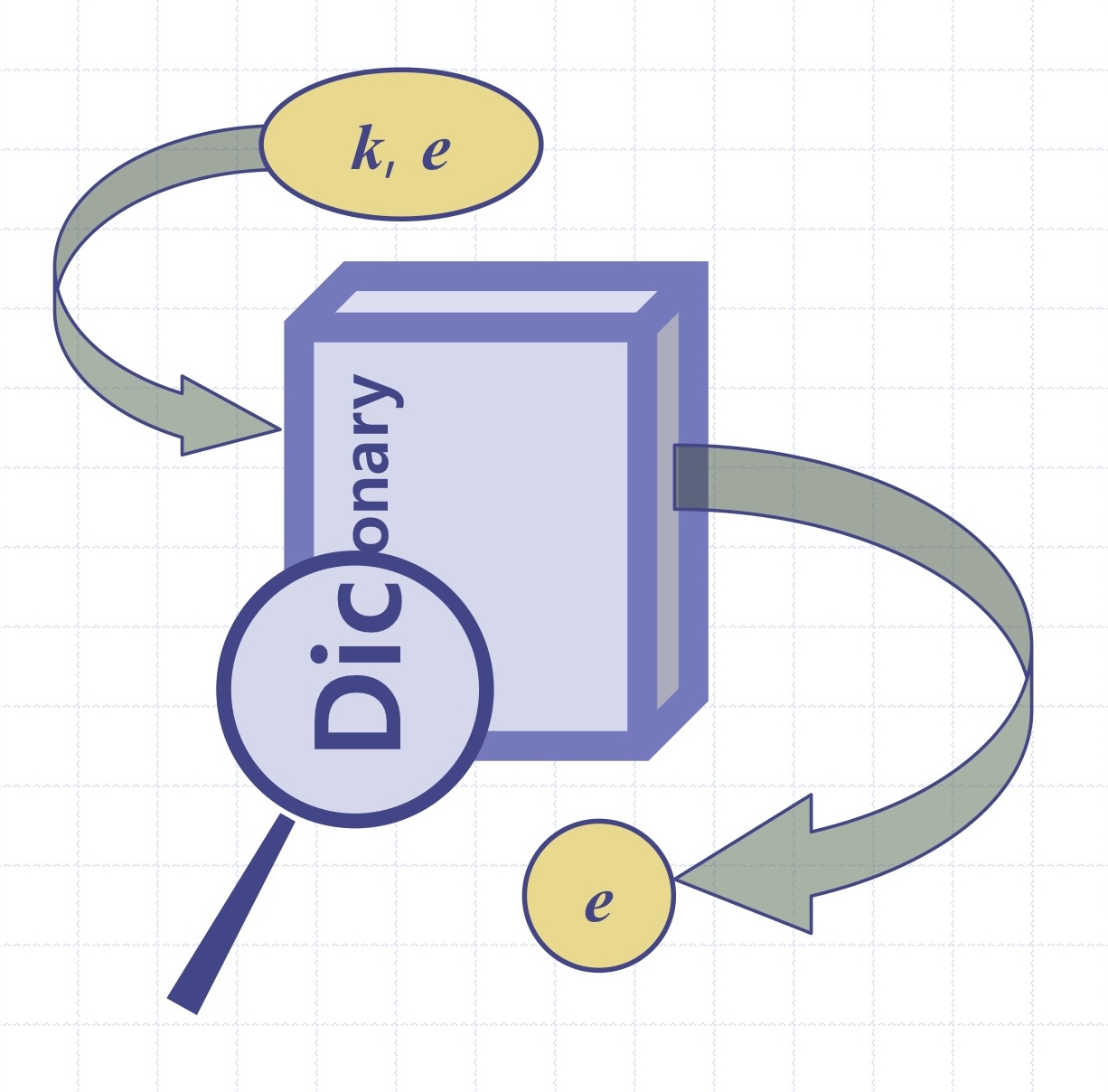
ㅇ사전(dictionary) ADT: 탐색 가능한 형태의 (key, value)쌍 항목들의 모음을 모델링
주로 해시 테이블(hash table)과 이진 검색 트리(BST)로 구현하며, 이때 각 키는 유일해야 한다 -> 유일키
- 직접응용: 연락처, 카드 사용승인, 인터넷주소 맵핑 e.g. www.sejong.ac.kr을 128.148.34.101로 맵핑
- 간접응용: 알고리즘 구현, 자료구조 구현
유일키(unique key): 한 개의 키에 대해 하나의 데이터만 존재
e.g. 학번, 계좌, ID
중복키(duplicate key): 한 개의 키에 대해 여러 개의 데이터가 존재
e.g. 이름, 나이, 계좌개설일자
[두 종류의 사전]
- 무순사전 ADT
- 순서사전 ADT
[사전 구현에 따른 탐색 기법]

"컴퓨터에서 정렬을 수행하는 이유 중 가장 큰 이유가 바로 이진 탐색이 가능한 데이터를 만들기 위해서이다"
ㅇ이진탐색(Binary Search): "up & down 게임"
상황) 0부터 12까지 중에 7을 검색
※ 이진탐색은 자료가 순서에 따라 정렬되어있어야 할 수 있다

시간복잡도: O(log(n))
이진탐색의 힘을 보여주는 예시로 스무고개가 있다
후보 범위가 100만 개가 넘더라도 이등분을 20회만 하면 1개 후보로 좁힐 수 있다
또다른 예시로는 전세계 인구가 토너먼트로 1등을 가려내기 위해서는 33회의 경기만 치루면 된다 ㅋㅋ..
(분할통치 vs 이진탐색)
분할통치: 이등분 된 두 개의 범위 양쪽을 모두 고려
이진탐색: 이등분 된 두 개의 범위 중 한쪽만 고려
ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ
이진탐색 활용) up & down 게임
[게임 규칙]
1. 친구는 두 개의 양의 정수 a와 b를 선택하고 세종이에게 알려준다. (단, a < b)
2. 친구는 a ≤ k ≤ b를 만족하는 정수 k를 하나 선택한다. (k는 세종이에게 알려주지 않는다)
3. 친구는 세종이에게 다음 정보를 알려준다. (이진 탐색)
- 친구는 세종이에게 k > m 인지, Y(예)/N(아니오)으로 알려준다.
(여기서 m은 a와 b사이의 중간값으로, m = ⌊(a + b) / 2⌋이다. ⌊⌋는 내림 기호)
- 답이 Y인 경우, m + 1 ≤ k ≤ b 이므로 a의 값을 m + 1로 바꾼다. 답이 N인 경우, a ≤ k ≤ m 이므로 b를 m으로 바꾼다.
- 위 과정을 a와 b가 같을 때까지 반복한다.
예) a = 10, b = 20이고, 3에서 주어지는 정보가 NNY인 경우
1) k>15인가? → 답) N ➜ 10≤k≤15
2) k>12인가? → 답) N ➜ 10≤k≤12
3) k>11인가? → 답) Y ➜ 12≤k≤12 (즉, k=12)
※ k를 찾기 위한 정확한 수의 답이 주어진다고 가정

(전체코드) - binarySearch() 함수 재귀버전
// up & down 게임
#include <stdio.h>
#include <stdlib.h>
int n;
char* YN;
int binarySearch(int a, int b, int idx);
int main() {
int a, b;
scanf("%d %d %d", &a, &b, &n);
YN = (char*)malloc((n + 1) * sizeof(char));
scanf("%s", YN);
printf("%d", binarySearch(a, b, 0));
free(YN);
return 0;
}
int binarySearch(int a, int b, int idx) {
int low = a, high = b;
if (idx == n) {
return low + (high - low) / 2; // (low + high) / 2 와 같다 (오버플로우 방지)
}
int mid = low + (high - low) / 2; // 중간값 갱신 (오버플로우 방지)
if (YN[idx] == 'Y') {
return binarySearch(mid + 1, high, idx + 1);
} else if (YN[idx] == 'N') {
return binarySearch(low, mid, idx + 1);
}
return -1; // 에러 처리
}
/*
10 20 3
NNY
1 1000 10
NYYNYNYYNY
*/
(전체코드) - binarySearch() 함수 비재귀버전
// up & down 게임
#include <stdio.h>
#include <stdlib.h>
int n;
char* YN;
int binarySearch(int a, int b);
int main() {
int a, b;
scanf("%d %d %d", &a, &b, &n);
YN = (char*)malloc((n + 1) * sizeof(char));
scanf("%s", YN);
printf("%d", binarySearch(a, b));
free(YN);
return 0;
}
int binarySearch(int a, int b) {
int low = a, high = b;
int mid = low + (high - low) / 2; // 중간값 계산 (오버플로우 방지)
for (int i = 0; i < n; i++) {
if (YN[i] == 'Y') {
low = mid + 1;
} else if (YN[i] == 'N') {
high = mid;
}
mid = low + (high - low) / 2; // 중간값 갱신 (오버플로우 방지)
}
return mid;
}
/*
10 20 3
NNY
1 1000 10
NYYNYNYYNY
*/
출처 및 참고: 알고리즘-원리와 응용(국형준교수님), Algorithm Design(Jon Kleinberg, Eva Tardos), Foundations of Algorithms using C++(Richard Neapolitan)
'Computer Science > 알고리즘' 카테고리의 다른 글
| [알고리즘] ep3+) 이진탐색트리(BST) 구현 (0) | 2024.07.17 |
|---|---|
| [알고리즘] ep3) 탐색트리 (0) | 2024.07.11 |
| [알고리즘] ep1-6+) 퀵정렬의 다양한 버전 (0) | 2024.07.10 |
| [알고리즘] ep1-4+) O(n + klog(n))의 힙정렬 (1) | 2024.07.10 |
| [알고리즘] 정렬 알고리즘 선택 매뉴얼 (1) | 2024.07.07 |

