다음의 문제 1과 문제 2는 주어진 그래프를 인접리스트 및 인접행렬로 각각 표현하여 해결해야 한다. 다음은 두 문제 모두에 공통된 사항이다.
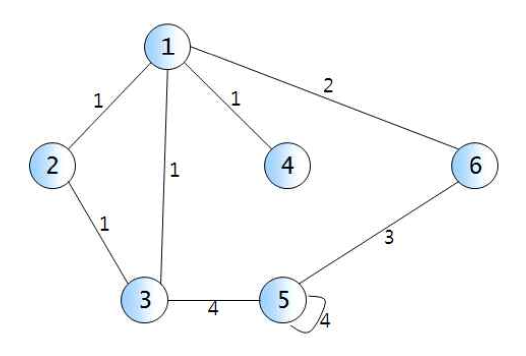
1) 그림 1의 그래프에 관해 해결해야 한다.
2) 가중치의 값은 양수와 음수 모두 가능하나, 0은 허용하지 않는다.
3) 그림 1 그래프의 정점 개수는 변경되지 않는다. 단, 간선 개수는 변화할 수 있다. 참고로 정점 6개인 그래프에서 가능한 간선 개수는, 자기 자신으로 가는 간선(즉, 루프)을 포함하여 최대 21(= 6 + 5 + 4 + 3 + 2 + 1)개다.
4) 간선의 이름을 생략하기로 한다. 따라서 간선 구조체의 이름 필드는 정의하지 않아도 된다.
5) 그래프를 배열 또는 연결리스트 가운데 어느 것을 이용하여 구현할지는 각자의 판단에 맡긴다.
문제1) 인접리스트 구현
그림의 무방향 가중그래프를 인접리스트로 표현하고, 다음
명령어에 따라 그래프 정보를 출력하거나 그래프를 수정하는 프로그램을 작성하시오.
대화식 프로그램에 주어지는 명령어는 a, m, q 세 가지며 각 명령에 대해 다음과 같이 수행해야 한다.
a <node number> : <node number>를 가지는 node와 인접한 node와 그 노드까지의 간선 가중치를 모두 인쇄. 단, node number의 오름차순으로 인쇄하되, space 외의 구분자 없이 노드번호 가중치 노드번호 가중치 ... 형식으로 인쇄한다. 그래프에 정점 a가 존재하지 않으면 아무 것도 하지 않고 –1을 출력한다.
m a b w : 간선 (a, b)의 가중치를 w로 변경한다. 그러한 간선이 존재하지 않을 때는 가중치 w인 새로운 간선 (a, b)를 생성한다. w = 0이면 간선 (a, b)를 삭제한다. 그래프에 정점 a 혹은 b가 존재하지 않으면 아무 것도 하지 않고 –1을 출력한다.
q : 프로그램 종료

(전체코드)
// 인접리스트 - 배열
#include <stdio.h>
#include <stdlib.h>
typedef struct INCIDENCE { // 간선의 정보를 저장하는 노드 구조체
int edgeIdx; // 간선의 인덱스
struct INCIDENCE* next; // 다음 간선 노드
} INCIDENCE;
typedef struct VERTEX {
int num;
INCIDENCE* incidence; // 정점에 부착된 간선 리스트의 헤드 포인터
} VERTEX;
typedef struct EDGE {
int u, v;
int w;
} EDGE;
typedef struct GRAPH {
VERTEX vertex[7]; // 정점 배열 (편의를 위해 인덱스를 1부터 시작)
EDGE edge[21]; // 간선 배열 (최대 간선 개수: 6 + 5 + 4 + 3 + 2 + 1 = 21)
int edgeSize; // 현재 간선의 개수
} GRAPH;
GRAPH* graph;
void initGraph();
INCIDENCE* getIncidence(int edgeIdx);
void insertIncidence(int u, int v, INCIDENCE* incidence);
void deleteIncidence(int u, int v);
void insertEdge(int u, int v, int w);
void updateEdge(int u, int v, int w);
void deleteEdge(int u, int v);
void printEdge(int u);
void freeGraph();
int main() {
char cmd;
int nodeNum;
int u, v;
int w;
initGraph();
while (1) {
scanf(" %c", &cmd);
if (cmd == 'a') { // 정점의 간선 정보 출력 명령
scanf("%d", &nodeNum);
printEdge(nodeNum);
}
else if (cmd == 'm') { // 간선 추가/수정/삭제 명령
scanf("%d %d %d", &u, &v, &w);
if (w != 0) { // 가중치가 0이 아니면 간선 추가/수정
updateEdge(u, v, w);
}
else if (w == 0) { // 가중치가 0이면 간선 삭제
deleteEdge(u, v);
}
}
else if (cmd == 'q') {
freeGraph();
break;
}
}
return 0;
}
void initGraph() {
graph = (GRAPH*)malloc(1 * sizeof(GRAPH));
graph->edgeSize = 0; // 초기 간선 개수 0으로 설정
for (int i = 1; i <= 6; i++) { // 각 정점 초기화
graph->vertex[i].incidence = NULL; // 간선 리스트 헤드 NULL로 초기화
graph->vertex[i].num = i; // 정점 번호 설정
}
// 초기 간선들 추가
insertEdge(1, 2, 1);
insertEdge(1, 3, 1);
insertEdge(1, 4, 1);
insertEdge(1, 6, 2);
insertEdge(2, 3, 1);
insertEdge(3, 5, 4);
insertEdge(5, 5, 4); // 자기 자신과 연결된 간선 (루프)
insertEdge(5, 6, 3);
}
INCIDENCE* getIncidence(int edgeIdx) {
INCIDENCE* node = (INCIDENCE*)malloc(1 * sizeof(INCIDENCE)); // 간선 노드 동적 할당
node->next = NULL; // 다음 노드 포인터 NULL로 초기화
node->edgeIdx = edgeIdx; // 간선 인덱스 설정
return node; // 간선 노드 반환
}
void insertIncidence(int u, int v, INCIDENCE* incidence) {
VERTEX* vertex = graph->vertex; // 정점 배열 포인터
EDGE* edge = graph->edge; // 간선 배열 포인터
INCIDENCE* ptr = vertex[u].incidence; // 현재 정점의 간선 노드 포인터 (간선 리스트 헤드 포인터)
if (ptr == NULL) { // 간선 리스트가 비어있을 경우
vertex[u].incidence = incidence; // 새로운 간선 노드를 헤드로 설정
return;
}
// 간선 리스트가 존재할 경우
int otherV; // 다른 정점 번호
if (edge[ptr->edgeIdx].u == u) {
otherV = edge[ptr->edgeIdx].v;
}
else {
otherV = edge[ptr->edgeIdx].u;
}
if (otherV > v) { // 새로운 간선 노드를 헤드로 교환
incidence->next = ptr;
vertex[u].incidence = incidence;
return;
}
// 오름차순으로 간선 노드 삽입
while (ptr->next != NULL) {
if (edge[ptr->next->edgeIdx].u == u) {
otherV = edge[ptr->next->edgeIdx].v;
}
else {
otherV = edge[ptr->next->edgeIdx].u;
}
if (otherV > v) {
break;
}
ptr = ptr->next;
}
incidence->next = ptr->next;
ptr->next = incidence;
}
void deleteIncidence(int u, int v) {
VERTEX* vertex = graph->vertex; // 정점 배열 포인터
EDGE* edge = graph->edge; // 간선 배열 포인터
INCIDENCE* ptr = vertex[u].incidence; // 현재 정점의 간선 노드 포인터 (간선 리스트 헤드 포인터)
if (ptr == NULL) { // 간선 리스트가 비어있을 경우
return;
}
// 헤드 간선 노드와 비교
int otherV; // 다른 정점 번호
if (edge[ptr->edgeIdx].u == u) {
otherV = edge[ptr->edgeIdx].v;
}
else {
otherV = edge[ptr->edgeIdx].u;
}
if (otherV == v) { // 헤드 간선 노드를 삭제할 경우
vertex[u].incidence = ptr->next; // 헤드 포인터를 다음 노드로 변경
free(ptr); // 기존 헤드 노드 메모리 해제
}
else { // 헤드가 아닌 간선 노드를 삭제할 경우
while (ptr->next != NULL) {
if (edge[ptr->next->edgeIdx].u == u) {
otherV = edge[ptr->next->edgeIdx].v;
}
else {
otherV = edge[ptr->next->edgeIdx].u;
}
if (otherV == v) {
break;
}
ptr = ptr->next;
}
if (ptr->next == NULL) { // 삭제할 노드가 없을 경우
return;
}
else { // 삭제할 노드를 재연결
INCIDENCE* temp = ptr->next;
ptr->next = ptr->next->next;
free(temp); // 삭제할 노드 메모리 해제
}
}
}
void insertEdge(int u, int v, int w) {
EDGE* edge = graph->edge; // 간선 배열 포인터
// 간선 배열에서 중복 검사 및 추가
for (int i = 0; i < graph->edgeSize; i++) {
if ((edge[i].u == u && edge[i].v == v)
|| (edge[i].u == v && edge[i].v == u)) {
edge[i].w = w; // 중복된 간선이 있으면 가중치 업데이트
return;
}
}
// 중복된 간선이 없는 경우
int idx = graph->edgeSize; // 새로운 간선 인덱스 설정
edge[idx].u = u; // 간선의 한쪽 정점 설정
edge[idx].v = v; // 간선의 다른쪽 정점 설정
edge[idx].w = w; // 간선의 가중치 설정
// 간선 노드 포인터 생성 및 추가
INCIDENCE* incidence1 = getIncidence(idx);
INCIDENCE* incidence2 = getIncidence(idx);
insertIncidence(u, v, incidence1);
if (u != v) { // 자기 자신과 연결된 간선이 아닐 경우
insertIncidence(v, u, incidence2);
}
graph->edgeSize++;
}
void updateEdge(int u, int v, int w) {
if (u < 1 || u > 6 || v < 1 || v > 6) {
printf("-1\n");
return;
}
EDGE* edge = graph->edge; // 간선 배열 포인터
INCIDENCE* ptr = graph->vertex[u].incidence; // 현재 정점의 간선 노드 포인터 (간선 리스트 헤드 포인터)
if (ptr == NULL) { // 간선 리스트가 비어있을 경우
insertEdge(u, v, w);
return;
}
int otherV; // 다른 정점 번호
int edgeFound = 0;
while (ptr != NULL) {
if (edge[ptr->edgeIdx].u == u) {
otherV = edge[ptr->edgeIdx].v;
}
else {
otherV = edge[ptr->edgeIdx].u;
}
if (otherV == v) { // 기존 간선의 가중치 변경
edge[ptr->edgeIdx].w = w;
edgeFound = 1;
break;
}
ptr = ptr->next;
}
if (edgeFound == 0) {
insertEdge(u, v, w);
}
}
void deleteEdge(int u, int v) {
if (u < 1 || u > 6 || v < 1 || v > 6) {
printf("-1\n");
return;
}
// 간선 배열은 insert에서 중복 검사를 수행하므로 따로 삭제하지 않음
// 간선 노드 삭제
deleteIncidence(u, v);
if (u != v) { // 자기 자신과 연결된 간선이 아닐 경우
deleteIncidence(v, u);
}
graph->edgeSize--;
}
void printEdge(int u) {
if (u < 1 || u > 6) {
printf("-1\n");
return;
}
VERTEX* vertex = graph->vertex; // 정점 배열 포인터
EDGE* edge = graph->edge; // 간선 배열 포인터
INCIDENCE* ptr = vertex[u].incidence; // 현재 정점의 간선 노드 포인터 (간선 리스트 헤드 포인터)
if (ptr == NULL) { // 간선 리스트가 비어있을 경우
return;
}
int otherV; // 다른 정점 번호
while (ptr != NULL) {
if (edge[ptr->edgeIdx].u == u) {
otherV = edge[ptr->edgeIdx].v;
}
else {
otherV = edge[ptr->edgeIdx].u;
}
printf(" %d %d", otherV, edge[ptr->edgeIdx].w); // 연결된 정점과 가중치 출력
ptr = ptr->next;
}
printf("\n");
}
void freeGraph() {
for (int i = 1; i <= 6; i++) {
INCIDENCE* cur = graph->vertex[i].incidence;
while (cur != NULL) {
INCIDENCE* temp = cur;
cur = cur->next;
free(temp);
}
}
free(graph);
}
/*
a 2
m 4 2 3
a 2
q
a 5
m 3 5 0
a 5
a 7
q
*/
문제2) 인접행렬 구현
그림의 무방향 가중그래프를 인접행렬로 표현하고, 명령어에 따라 그래프 정보를 인쇄하거나 그래프를 수정하는 프로그램을 작성하시오. 명령어 정의와 입출력 예시는 문제1과 같다.
(전체코드)
// 인접행렬 - 배열
#include <stdio.h>
#include <stdlib.h>
typedef struct EDGE {
int u, v;
int w;
} EDGE;
typedef struct GRAPH {
int vertex[6];
EDGE edge[21];
int adjacency[6][6]; // 인접행렬: 간선 인덱스를 저장하며 초기값은 -1이다
int edgeSize; // 현재 간선의 개수
} GRAPH;
GRAPH* graph;
void initGraph();
void insertEdge(int u, int v, int w);
void updateEdge(int u, int v, int w);
void deleteEdge(int u, int v);
void printEdge(int u);
int main() {
char cmd;
int nodeNum;
int u, v;
int w;
initGraph();
while (1) {
scanf(" %c", &cmd);
if (cmd == 'a') { // 정점의 간선 정보 출력 명령
scanf("%d", &nodeNum);
printEdge(nodeNum - 1);
}
else if (cmd == 'm') { // 간선 추가/수정/삭제 명령
scanf("%d %d %d", &u, &v, &w);
if (w != 0) { // 가중치가 0이 아니면 간선 추가/수정
updateEdge(u - 1, v - 1, w);
}
else if (w == 0) { // 가중치가 0이면 간선 삭제
deleteEdge(u - 1, v - 1);
}
}
else if (cmd == 'q') {
break;
}
}
free(graph);
return 0;
}
void initGraph() {
graph = (GRAPH*)malloc(1 * sizeof(GRAPH));
graph->edgeSize = 0;
for (int i = 0; i < 6; i++) {
graph->vertex[i] = i;
for (int j = 0; j < 6; j++) {
graph->adjacency[i][j] = -1; // 가중치가 0일 수 있으니 -1로 초기화
}
}
insertEdge(1 - 1, 2 - 1, 1);
insertEdge(1 - 1, 3 - 1, 1);
insertEdge(1 - 1, 4 - 1, 1);
insertEdge(1 - 1, 6 - 1, 2);
insertEdge(2 - 1, 3 - 1, 1);
insertEdge(3 - 1, 5 - 1, 4);
insertEdge(5 - 1, 5 - 1, 4);
insertEdge(5 - 1, 6 - 1, 3);
}
void insertEdge(int u, int v, int w) {
EDGE* edge = graph->edge;
// 간선 배열에서 중복 검사 및 추가
for (int i = 0; i < graph->edgeSize; i++) {
if ((edge[i].u == u && edge[i].v == v)
|| (edge[i].u == v && edge[i].v == u)) {
edge[i].w = w; // 중복된 간선이 있으면 가중치 업데이트
return;
}
}
// 중복된 간선이 없는 경우
int idx = graph->edgeSize; // 새로운 간선 추가를 위한 인덱스
edge[idx].u = u;
edge[idx].v = v;
edge[idx].w = w;
// 인접 행렬 업데이트
// 인접 행렬에 간선 인덱스를 저장
graph->adjacency[u][v] = idx;
graph->adjacency[v][u] = idx;
graph->edgeSize++;
}
void updateEdge(int u, int v, int w) {
if (u < 0 || u > 5 || v < 0 || v > 5) {
printf("-1\n");
return;
}
EDGE* edge = graph->edge;
if (graph->adjacency[u][v] == -1) { // 간선이 없으면 간선 추가
insertEdge(u, v, w);
} else { // 간선이 있으면 가중치 업데이트
edge[graph->adjacency[u][v]].w = w;
}
}
void deleteEdge(int u, int v) {
if (u < 0 || u > 5 || v < 0 || v > 5) {
printf("-1\n");
return;
}
// 간선 삭제(인접 행렬에서)
// edge list는 insert에서 중복 검사하므로 따로 삭제 X
graph->adjacency[u][v] = -1;
graph->adjacency[v][u] = -1;
graph->edgeSize--;
}
void printEdge(int u) {
if (u < 0 || u > 5) {
printf("-1\n");
return;
}
EDGE* edge = graph->edge;
int idx;
for (int i = 0; i < 6; i++) {
idx = graph->adjacency[u][i]; // 인접 행렬에서 간선 인덱스 가져오기
if (idx == -1) { // 간선이 없는 경우
continue;
}
printf(" %d %d", i + 1, edge[idx].w);
}
printf("\n");
}
/*
a 2
m 4 2 3
a 2
q
a 5
m 3 5 0
a 5
a 7
q
*/
https://www.youtube.com/watch?v=D_ZuvwIkinQ&list=PLFgS-xIWwNVX-zm4m6suWC9d7Ua9z7fuT&index=28
그래프 구현에 관해서 이 영상을 참고하자! 아주 좋은 영상이다
출처 및 참고: 알고리즘-원리와 응용(국형준교수님), Algorithm Design(Jon Kleinberg, Eva Tardos), Foundations of Algorithms using C++(Richard Neapolitan)
'Computer Science > 알고리즘' 카테고리의 다른 글
| [알고리즘] ep5-2+) DFS, BFS 구현 (1) | 2024.07.22 |
|---|---|
| [알고리즘] ep5-2) 그래프 순회 (1) | 2024.07.21 |
| [알고리즘] ep5-1) 그래프(graph) (0) | 2024.07.21 |
| [알고리즘] ep4+++) 비활성화 방식 삭제 (0) | 2024.07.19 |
| [알고리즘] ep4++) 개방주소법 구현(선형 조사, 이중 해싱) (3) | 2024.07.19 |



