[알고리즘] ep5-1) 그래프(graph)

ㅁ그래프(graph) ADT: (vertex, edge)의 쌍

v: 정점 노드들의 집합

e: 간선 노드들의 집합

항공편의 그래프 예시

 

정점: 공항을 표현하며 공항도시 이름을 저장

간선: 두 공항 사이의 항로를 표현하며 항로의 거리(mile)를 저장

 

 

[그래프 응용]

- 전자회로: 인쇄회로기판(PCB), 집적회로(IC)

- 교통망: 고속도로망, 항공노선망

- 컴퓨터 네트워크: LAN, 인터넷, 웹

- 데이터베이스: 개체-관계 다이어그램(entity-relationship diagram)

 

 

 

ㅇ무방향그래프(undirected graph): 모든 간선이 무방향간선인 그래프

무방향간선(undirected edge)

 

 

ㅇ방향그래프(directed graph): 모든 간선이 방향간선인 그래프

방향간선(directed edge)

 

 

[그래프 기본 용어]

간선의 끝점(end vertex or endpoint): 점점 U와 V는 a의 양 끝점

정점의 부착(incident) 간선: a, d, b는 V에 부착한다

정점의 인접(adjacent) 정점: U와 V는 인접하다

정점의 차수(degree): X의 차수는 5다

병렬 간선(parallel edges): h와 i는 병렬 간선

루프(loop or self-loop): j는 루프다

 

경로(path)

- 정점과 간선의 교대열 (그래프의 정점과 간선이 번갈아 나오는 형태)

- 정점으로 시작하여 정점으로 끝난다

- 각 간선은 그 양 끝점으로 시작하고 끝난다 (간선의 양 끝점이 해당 간선의 시작과 끝을 의미한다)

단순경로(simple path): 모든 정점과 간선이 유일한 경로

 

싸이클(cycle)

- 정점과 간선이 교대하는 원형열

- 각 간선은 그 양 끝점으로 시작하고 끝난다 (간선의 양 끝점이 해당 간선의 시작과 끝을 의미한다)

단순싸이클(simple cycle): 모든 정점과 간선이 유일한 싸이클

 

 

 

 

신장 부그래프가 부그래프의 상위 개념이다

 

ㅇ부그래프(subgraph)

정점: v의 부분집합

간선: e의 부분집합

 

ㅇ신장 부그래프(spanning subgraph)

정점: v

간선: e의 부분집합

 

 

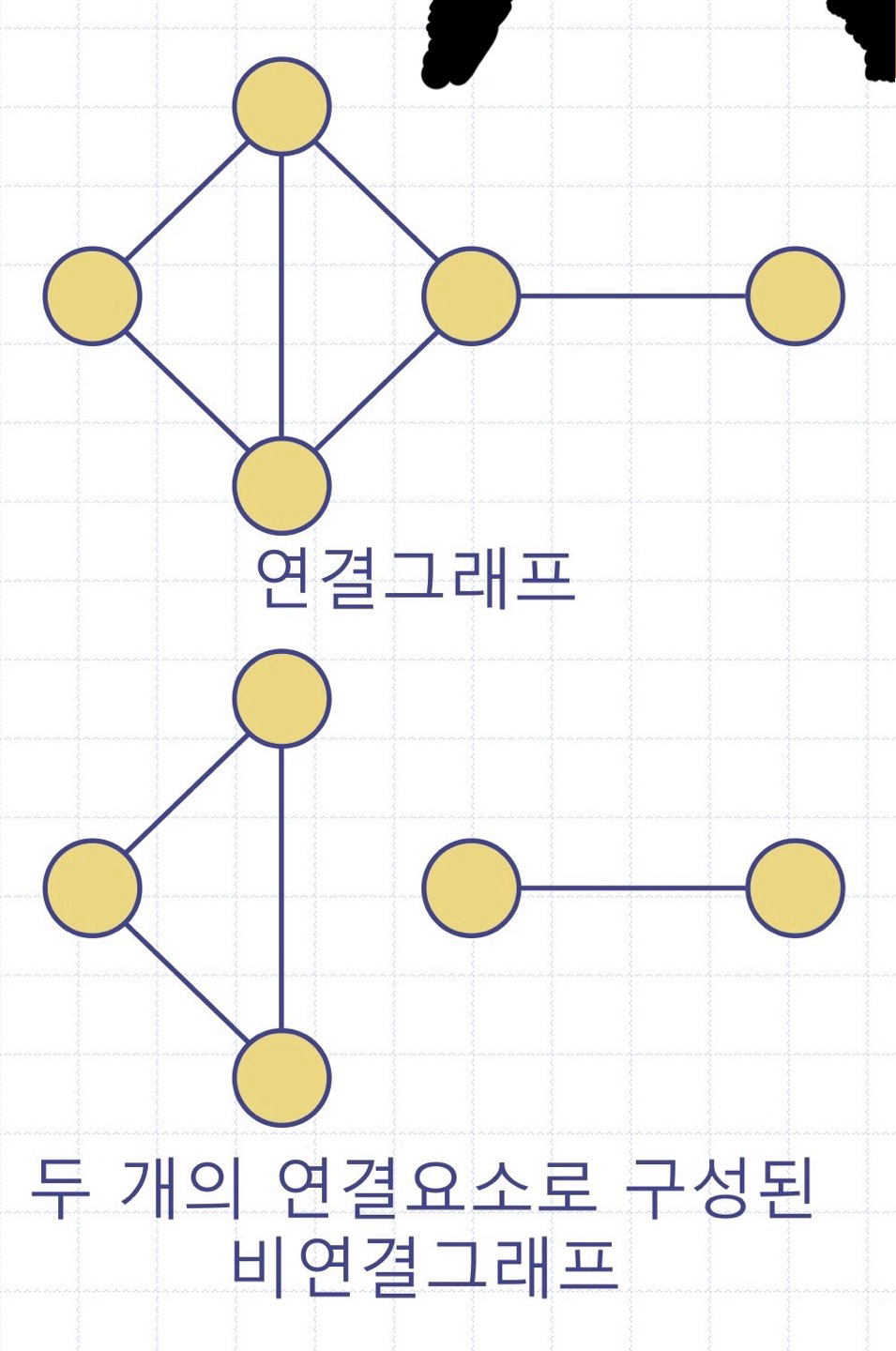
모든 정점쌍에 대해 경로가 존재하면 "그래프가 연결(connected)되었다"라고 말한다

그래프 G의 연결요소(connected component): G의 최대 연결 부그래프

 

 

희소 그래프(sparse graph)와 밀집 그래프(dense graph)

 

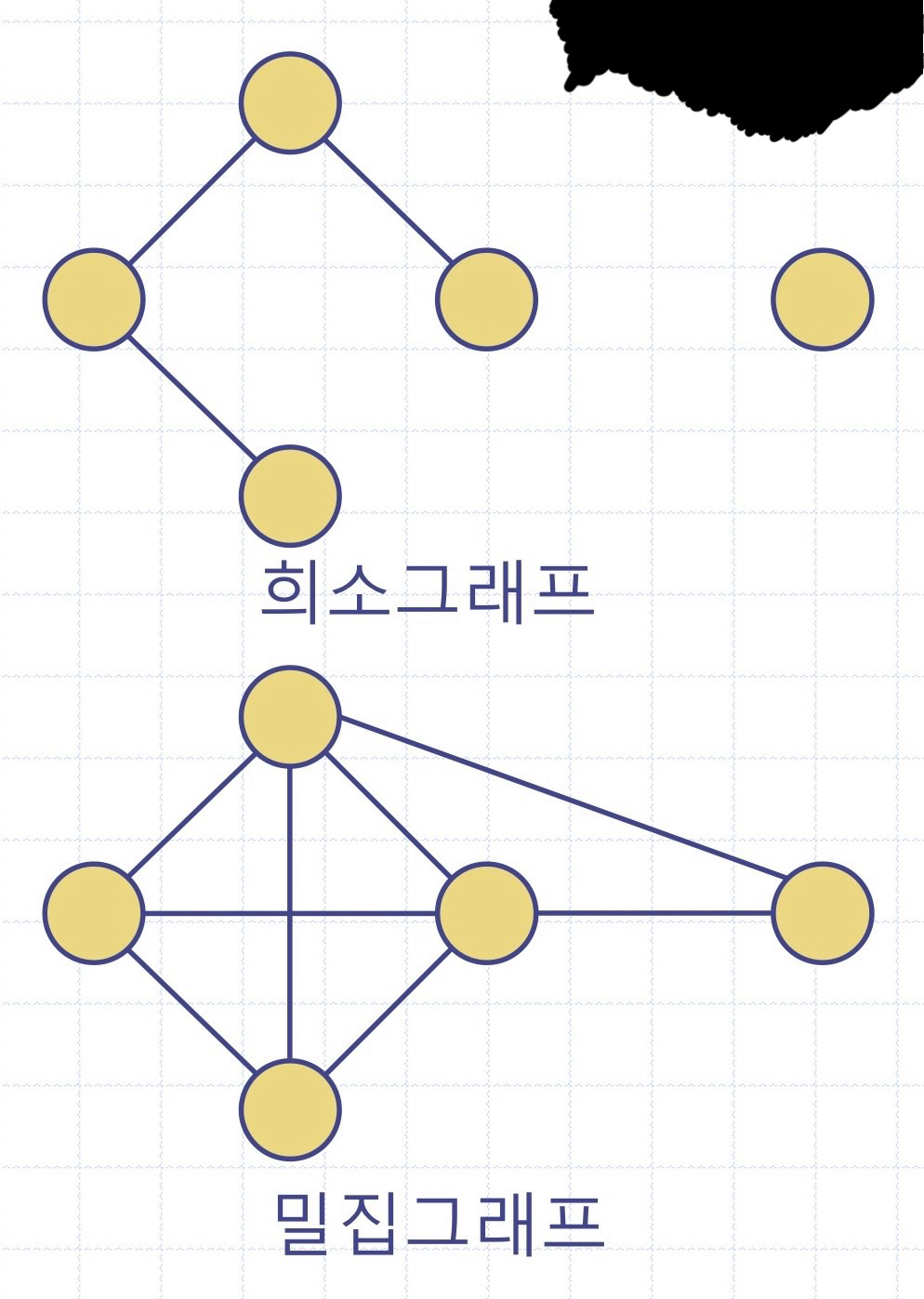
그래프 알고리즘의 선택은 종종 간선의 밀집도(density)에 따라 좌우된다

 

상황) 알고리즘 A의 시간복잡도: O(nm) / 알고리즘 B의 시간복잡도: O(n^2)

- 만약 그래프 G가 희소(sparse)하다면, 알고리즘 A가 B보다 빠르다

- 만약 그래프 G가 밀집(dense)하다면, 알고리즘 B가 A보다 빠르다

 

 

숲의 연결요소가 트리들이다

 

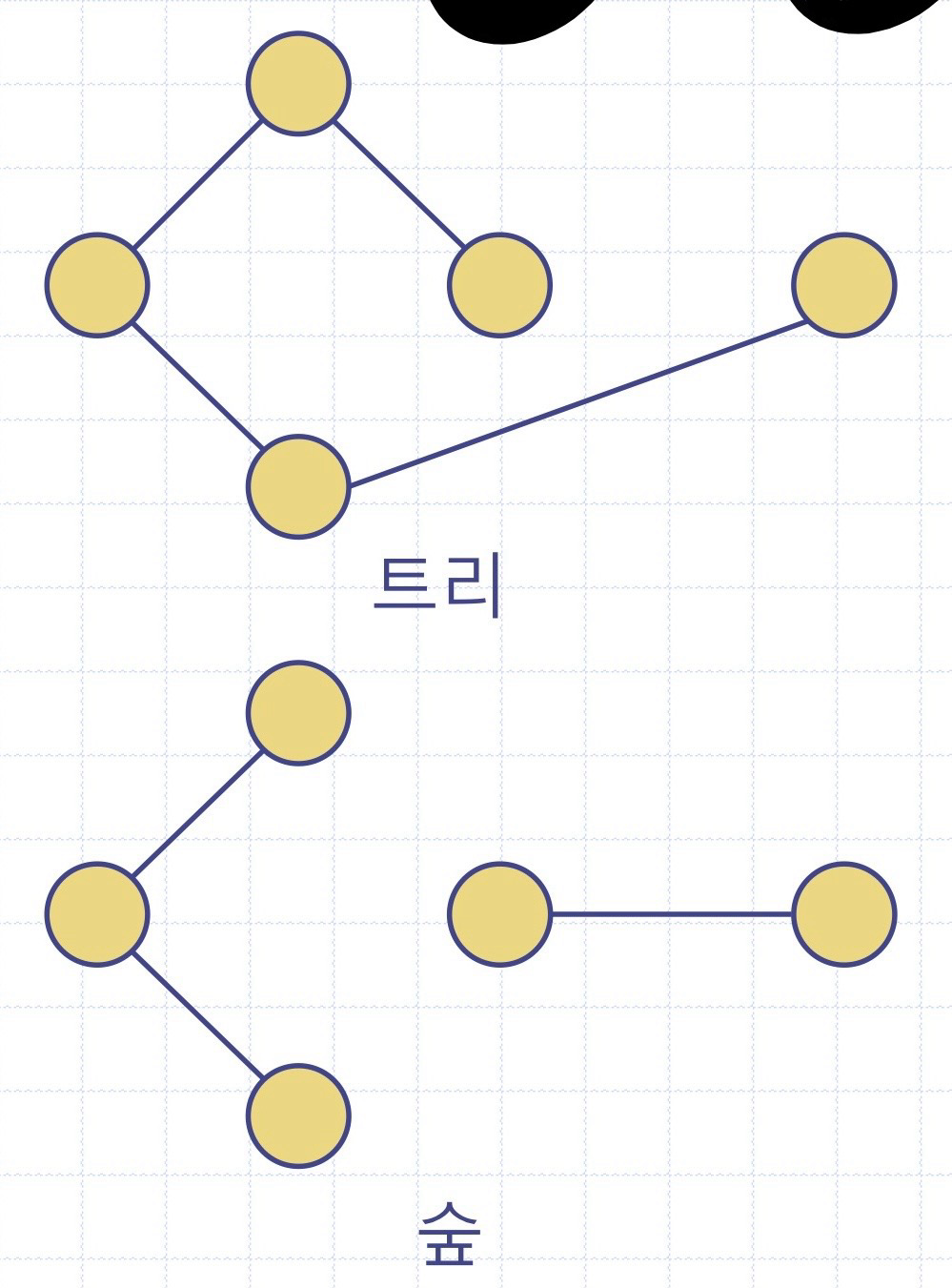
ㅇ자유 트리(free tree) or 트리(tree): 다음 조건을 만족하는 무방향그래프 T

- T는 연결됨

- T에 싸이클이 존재하지 않음

(위 트리에 대한 정의는 루트가 있는 트리에 대한 정의와는 다르다)

 

ㅇ숲(forest): 싸이클이 없는 무방향그래프

 

 

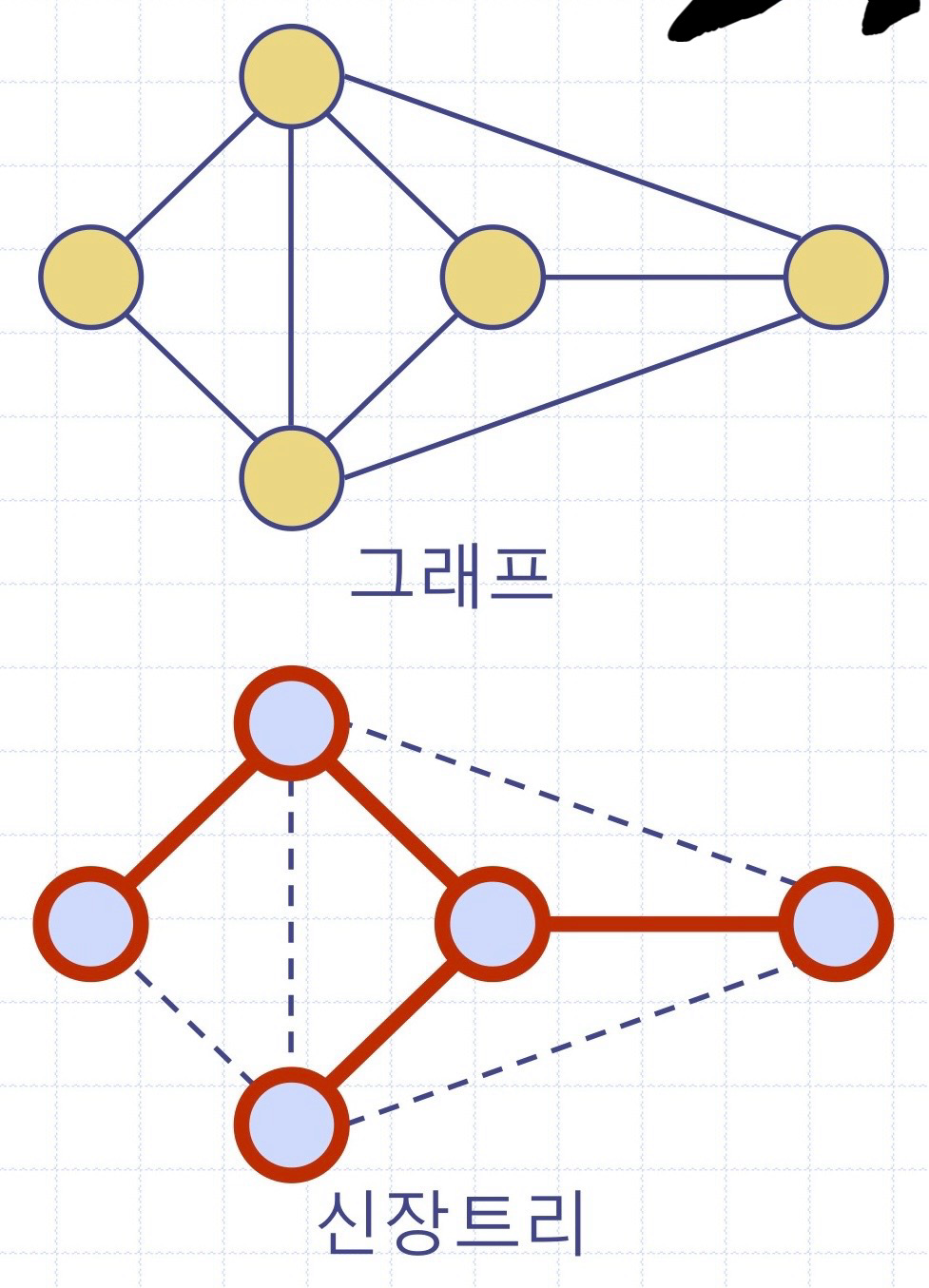
ㅇ신장 트리(spanning tree): 신장 부그래프 가운데 트리인 것

- 신장 트리는 그래프가 트리가 아닌 한, 유일하지 않다

- 신장 트리는 통신망 설계에 응용된다

 

ㅇ신장 숲(spanning): 신장 부그래프 가운데 숲인 것

 

 

 

 

[그래프의 속성]

n: 정점 수

m: 간선 수

deg(v): 정점 v의 차수

 

속성 1)

3 + 3 + 3 + 3 = 2 x 6

 

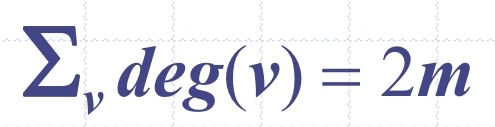
증명: 각 간선이 두 번 세어진다

 

속성 2)

조건: 루프와 병렬 간선이 없는 무방향그래프

 

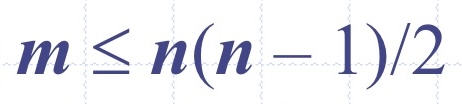
증명: 각 정점의 최대 차수는 (n - 1)

 

 

<예시>

그래프 예시

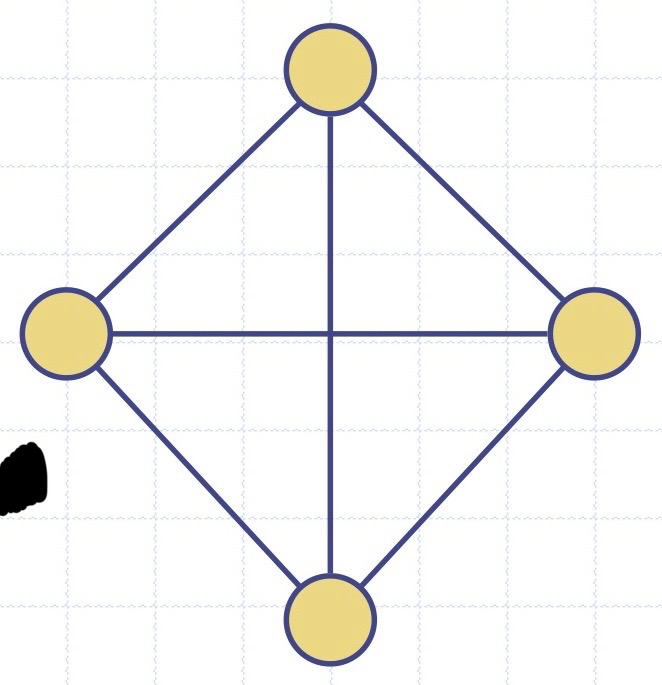
n = 4

m = 6

deg(v) = 3

 

그렇다면 여기서 질문을 하나 던지고 싶다

방향그래프에서의 m의 상한은 과연 어떨까?

 

 

 

 

그래프 구현 방식에는 인접리스트, 인접행렬 두 가지 방식이 있으며, 두 가지 방식 모두 간선리스트(edge list)를 기본으로 갖는다

간선리스트 구조

 

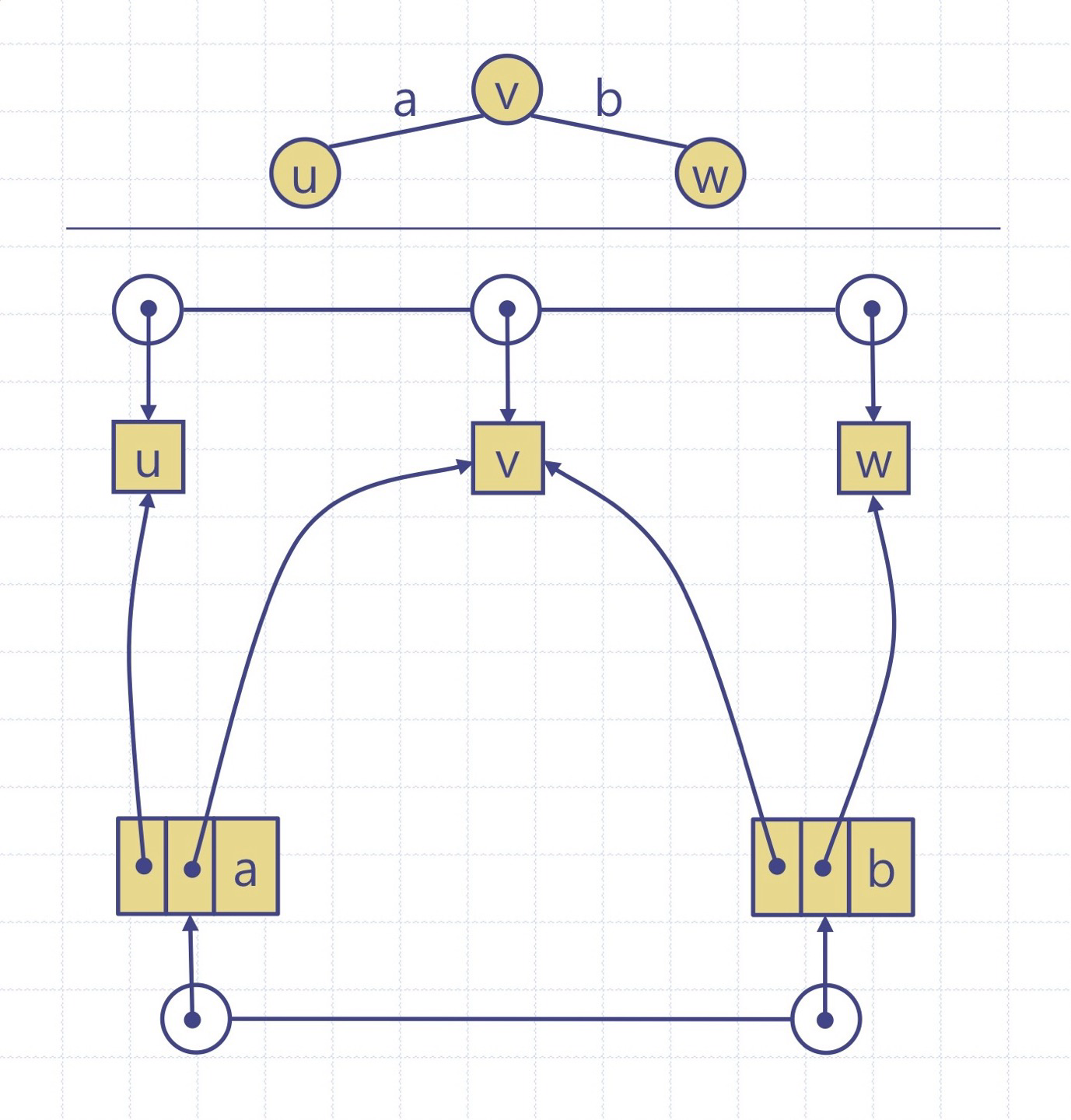
정점리스트

- 정점 노드들에 대한 포인터의 리스트

간선리스트

- 간선 노드들에 대한 포인터의 리스트

정점 노드

- 원소

간선 노드

- 원소

- 시점 노드

- 종점 노드

 

 

1. 인접리스트(adjacency list) 구조 

각 정점에 대한 부착리스트(incident list)

각 정점의 부착간선들을 간선노드에 대한 참조들의 리스트로 표시

 

 

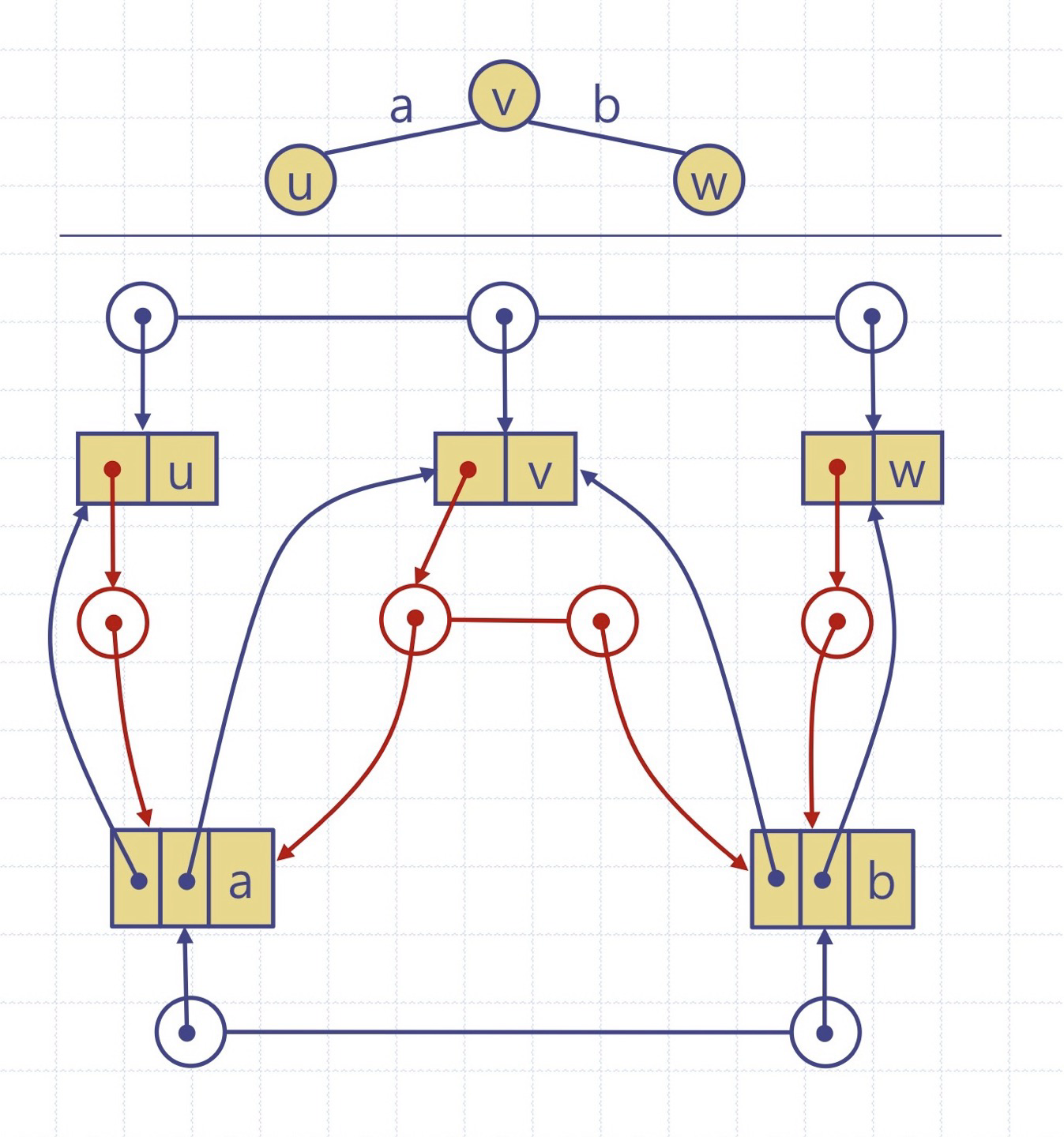
2. 인접행렬(adjacency matrix) 구조

n x n의 인접행렬(adjacency matrix)

- 인접정점 쌍에 대응하는 간선 노드들에 대한 참조

- 비인점정점 쌍에 대해서는 NULL 정보를 저장한다

(구식 버전은 간선의 존재여부만을 1 or 0으로 저장)

 

 

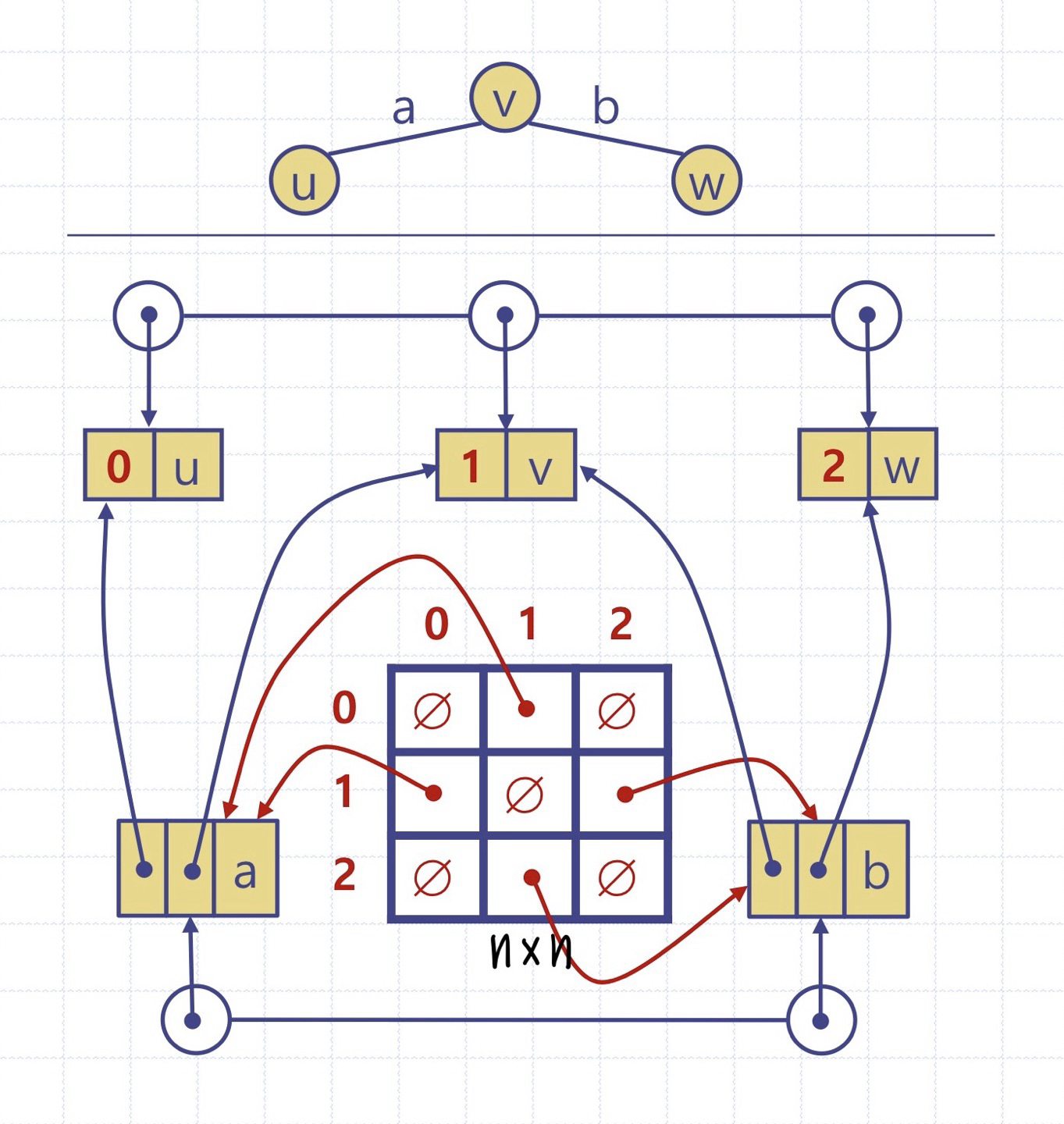
우리는 이 두 가지 구조를 연결리스트 or 배열로 구현할 수 있다

[연결리스트를 이용한 상세 구현]

 

 

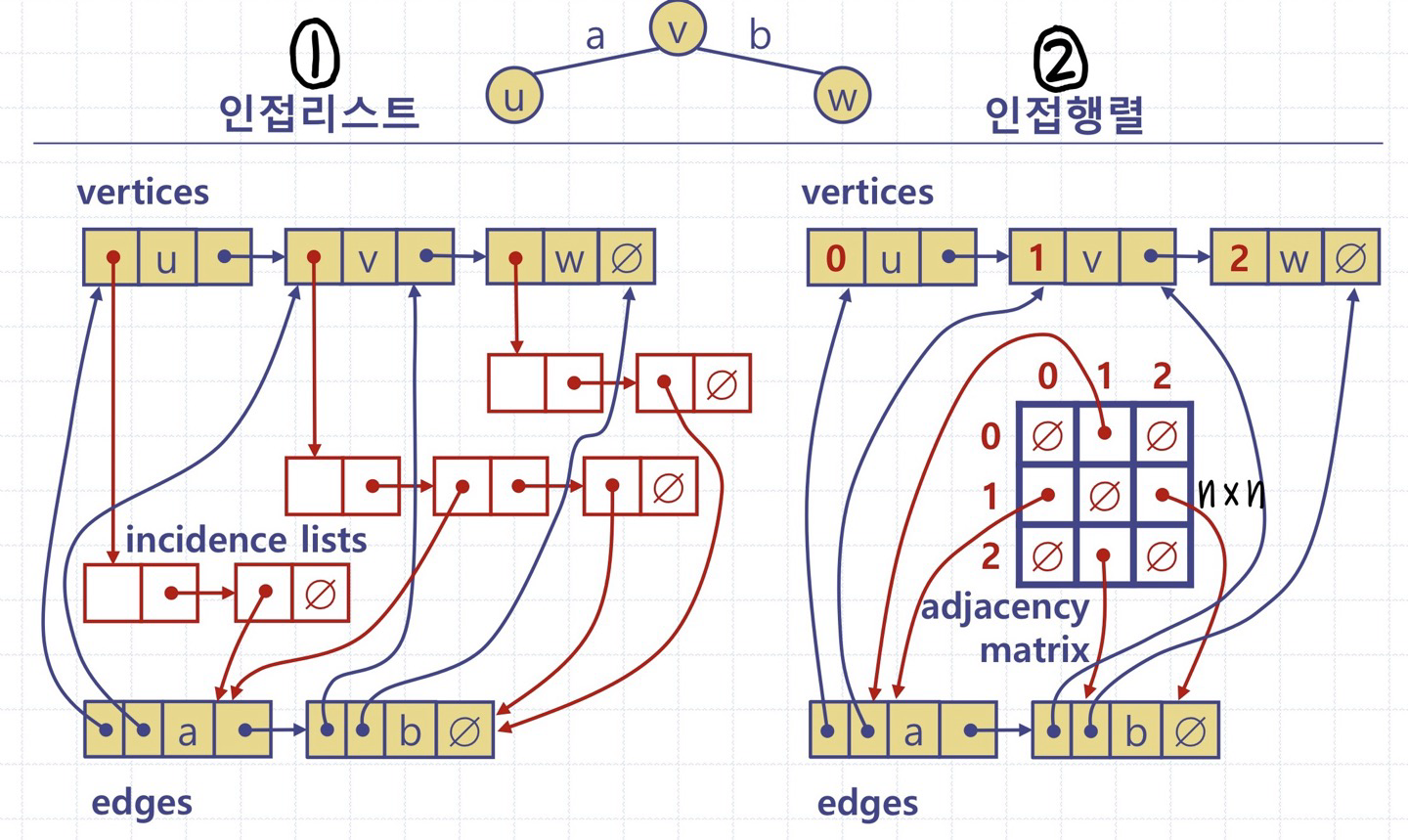
[배열을 이용한 상세 구현]

 

 

 

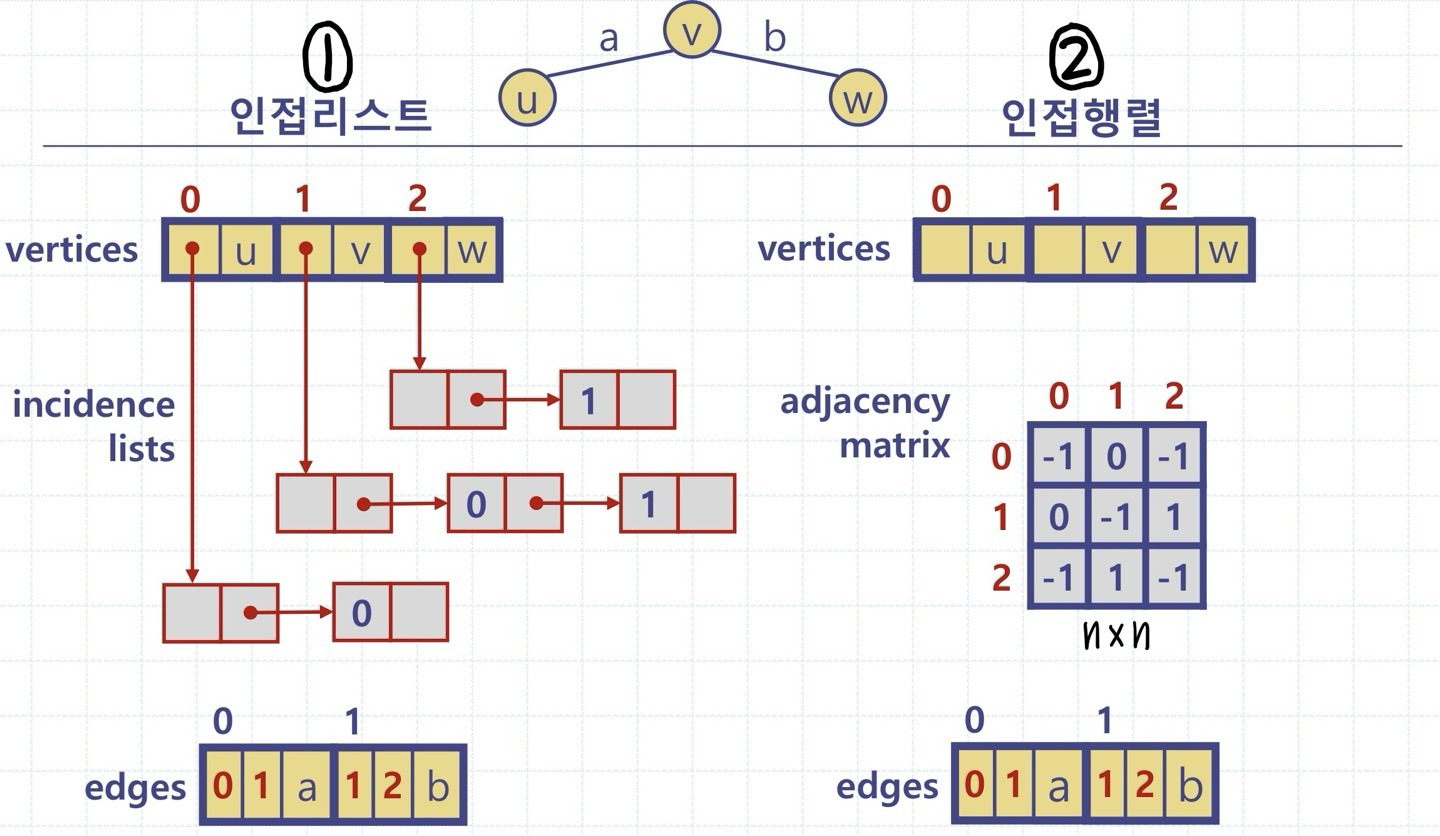
[그래프 상세 구현 비교]

 

점근 성능

 

 

 

 

 

 

 

 

 

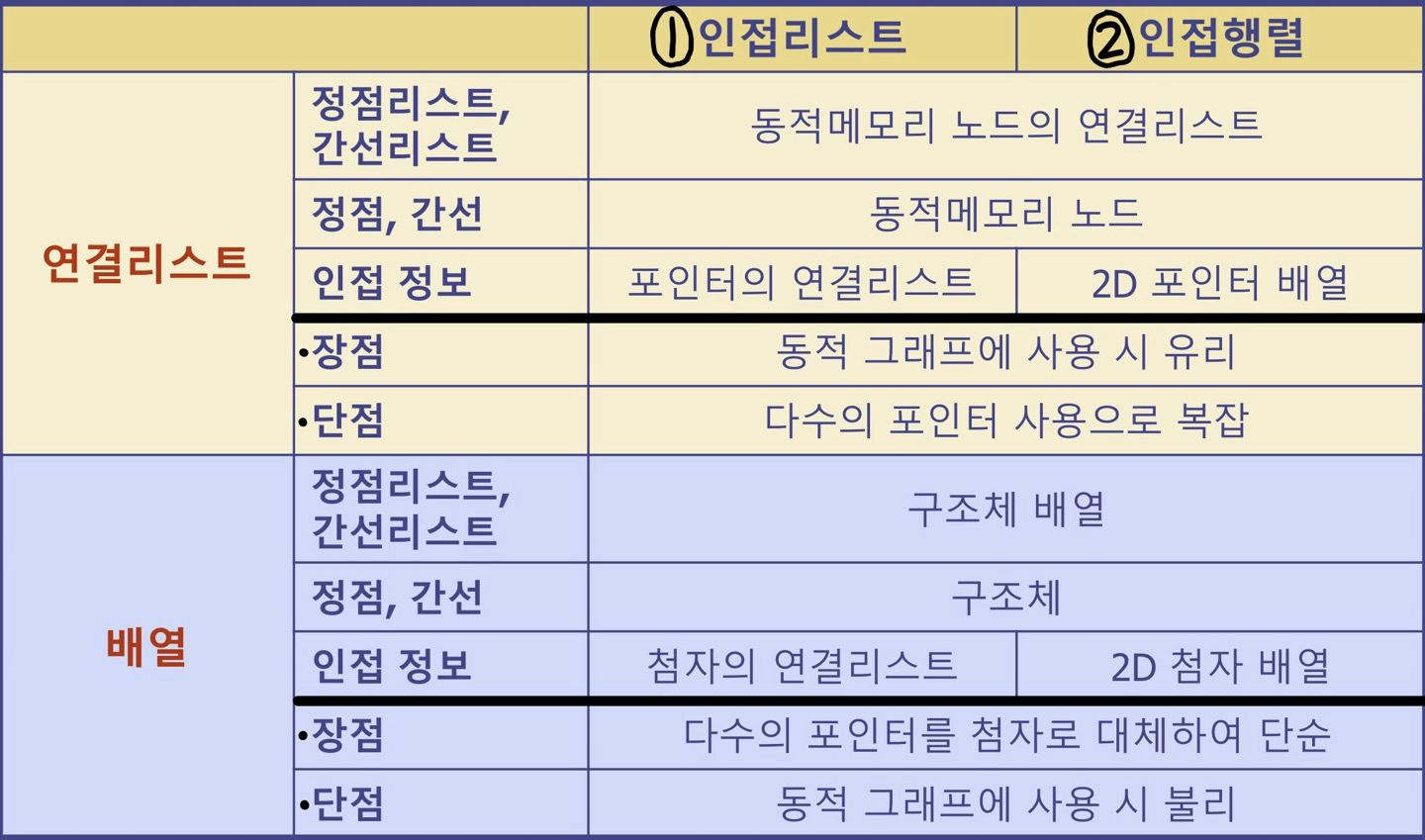
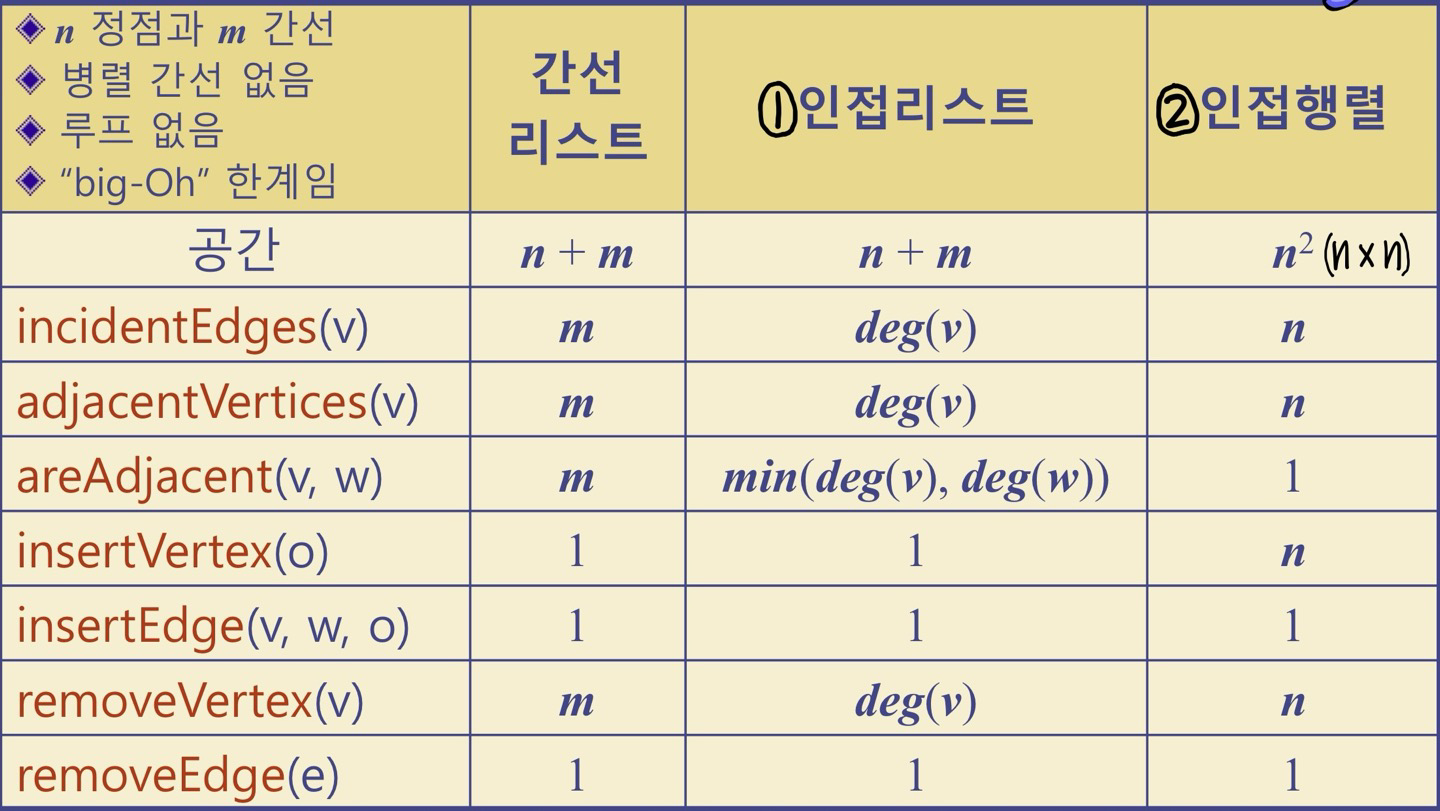
출처 및 참고: 알고리즘-원리와 응용(국형준교수님), Algorithm Design(Jon Kleinberg, Eva Tardos), Foundations of Algorithms using C++(Richard Neapolitan)