그래프 순회(graph traversal): 모든 정점과 간선을 검사함으로써 그래프를 탐험하는 체계적인 절차
<순회의 예시>
- 수도권 전철망의 모든 역(정점)의 위치를 출력
- 항공사의 모든 항공편(간선)에 대한 노선 정보를 수집
- 웹 검색엔진의 데이터 수집 부문은 웹의 하이퍼텍스트 문서(정점)와 문서 내 링크(간선)를 검사함으로써 서핑
그래프의 순회로는 DFS, BFS 두 가지가 있다
그래프 G에 대한 DFS 순회 또는 BFS 순회의 활용은 아래와 같다
- G의 모든 정점과 간선을 방문
- G가 연결그래프인지 결정
- G의 연결요소들을 계산
- G의 신장 숲을 계산
① 깊이우선탐색(DFS, Depth-First Search) by 스택(재귀)
n개의 정점과 m개의 간선을 가진 그래프에 대한 DFS는 O(n + m) 시간 소요
"DFS는 모든 경로를 추적하는 데 유용하다"
(DFS를 확장하여 해결할 수 있는 문제들)
- 두 개의 주어진 정점 사이의 경로를 찾아 보고
- 연결성 검사
- 경로 찾기
- 싸이클 찾기
DFS 과정은 선위순회와 유사하다
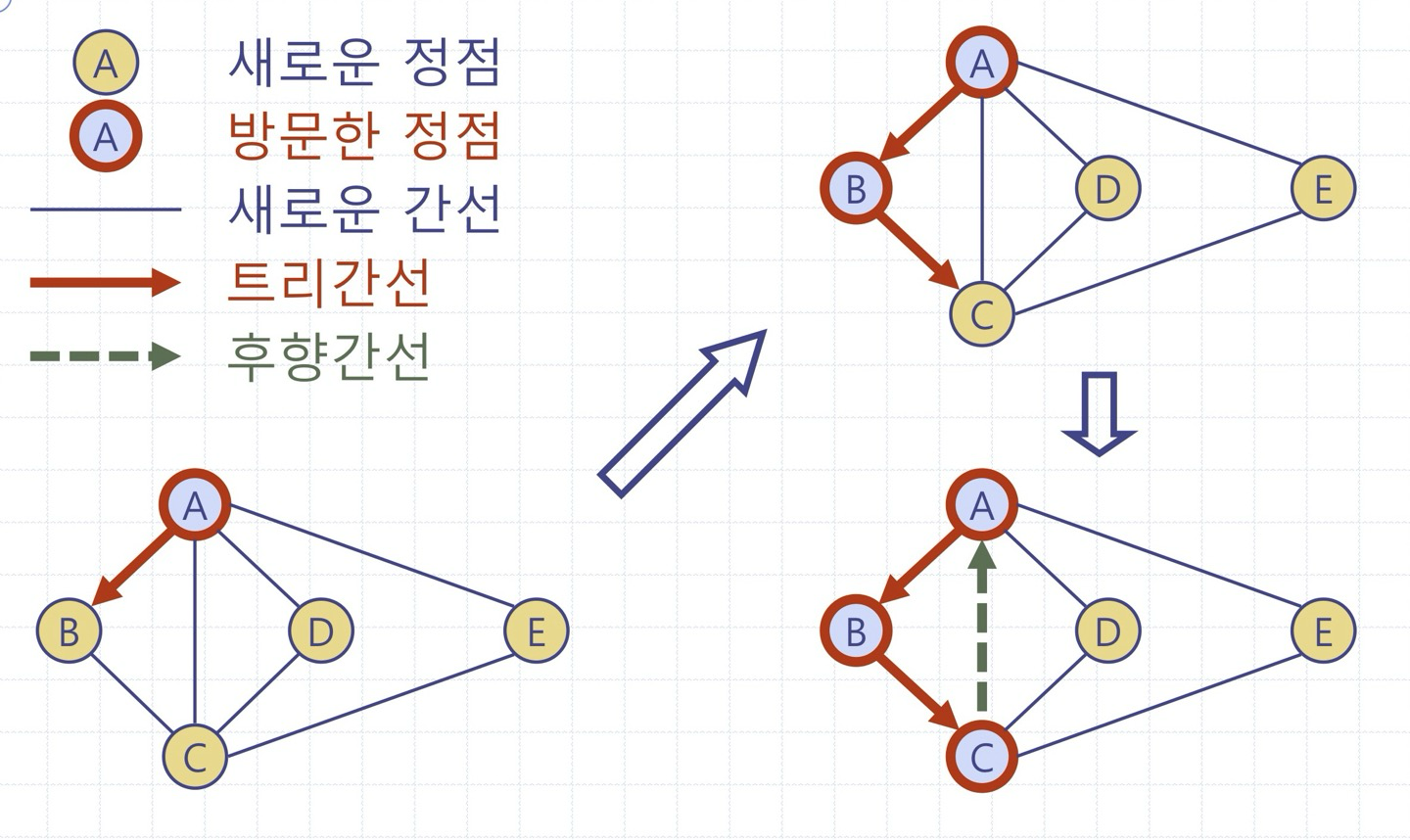

DFS 알고리즘은 미로를 탐험하는 데에 있어서 고전적이고 모험적인 전략과 유사하다
- 방문한 교차로, 모퉁이, 막힌 복도를 표시(모두 정점)
- 순회한 복도를 표시(모두 간선)
- 입구(출발정점)로 되돌아가는 경로를 끈(재귀스택)을 사용하여 추적

[DFS 속성]

속성 1)
rDFS(G, v)는 v의 연결요소 내의 모든 정점과 간선을 방문
속성 2)
rDFS(G, v)에 의해 라벨 된 트리 간선들은 v의 연결요소의 신장 트리(DFS tree라 칭한다)를 형성
[DFS 분석]
정점과 간선의 라벨을 쓰고 읽는데 O(1)시간 소요
*라벨(label): 방문 여부 플래그
각 정점은 두 번 라벨 된다
- 한 번은 Fresh로, 또 한 번은 Visited로
각 간선은 두 번 라벨 된다
- 한 번은 Fresh로, 또 한 번은 Tree 또는 Back으로
그래프가 "인접리스트 구조"로 구현된 경우, DFS는 O(n + m) 시간에 수행된다
② 너비우선탐색(BFS, Breadth-First Search) by 큐
n개의 정점과 m개의 간선을 가진 그래프에 대한 BFS는 O(n + m) 시간 소요
"BFS는 최단 경로를 찾는 데 유용하다"
(BFS를 확장하여 해결할 수 있는 문제들)
- 두 개의 주어진 정점 사이의 최소 간선을 사용하는 경로를 찾아보고 (또는 그런 경로가 없음을 보고)
- G가 숲임을 보고
BFS 과정은 레벨순회와 유사하다

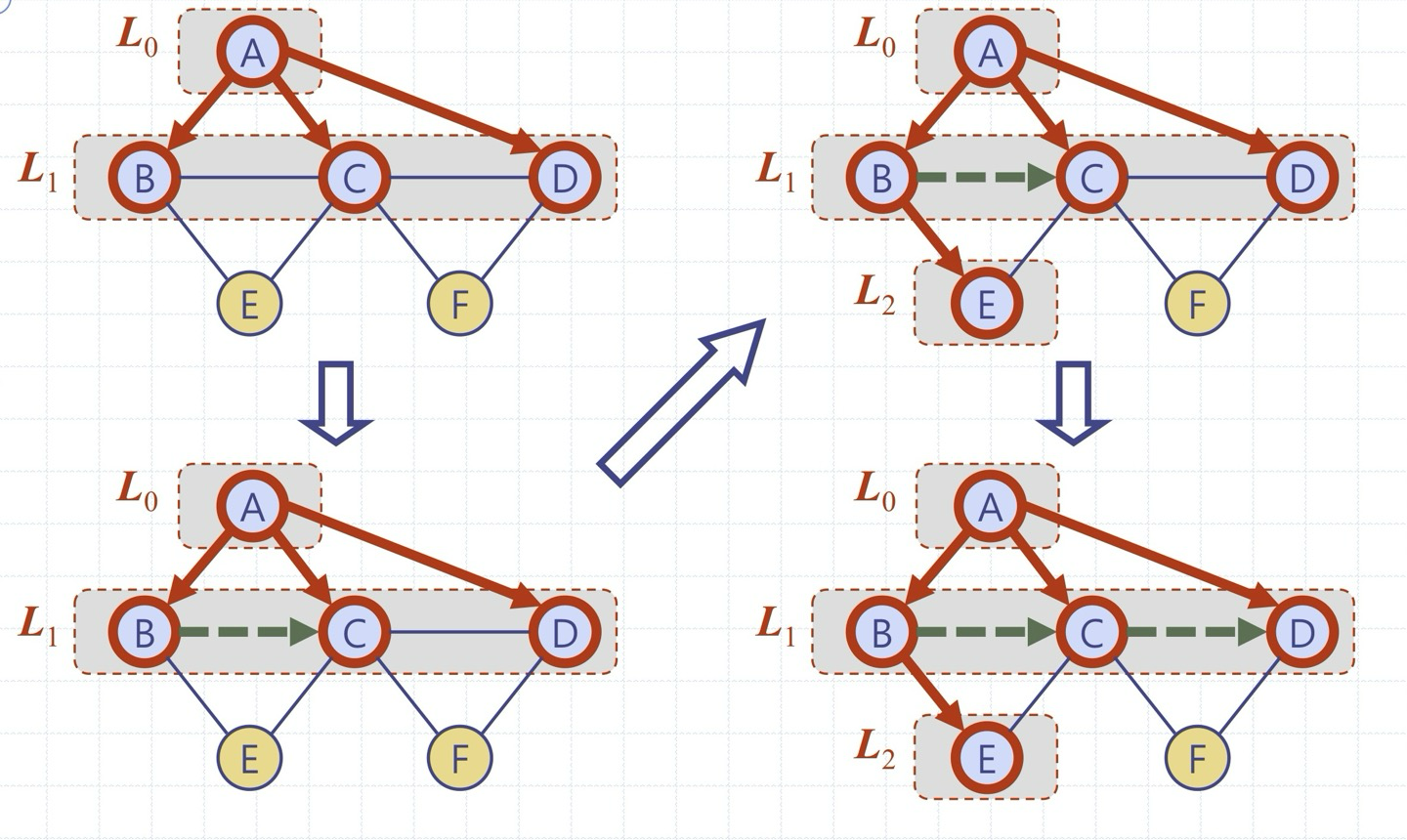

BFS 알고리즘은 미로를 탐험하는 데에 있어서 보수적인 전략과 유사하다
- 방문한 교차로, 모퉁이, 막힌 복도를 표시(모두 정점)
- 순회한 복도를 표시(모두 간선)
- 레벨을 하나씩 증가시키면서 진행

[BFS 속성]

속성 1)
BFS(G, v)는 v의 연결요소 내의 모든 정점과 간선을 방문
속성 2)
BFS(G, v)에 의해 라벨 된 트리 간선들은 v의 연결요소의 신장 트리(BFS tree라 칭한다)를 형성
+ 속성 3)
Li내의 각 정점 w에 대해
- BFS tree의 v에서 w로 향하는 경로는 i개의 간선을 가진다
- v의 연결요소 내의 v에서 w로 향하는 모든 경로는 최소 i개의 간선을 가진다
[BFS 분석]
정점과 간선의 라벨을 쓰고 읽는데 O(1)시간 소요
*라벨(label): 방문 여부 플래그
각 정점은 두 번 라벨 된다
- 한 번은 Fresh로, 또 한 번은 Visited로
각 간선은 두 번 라벨 된다
- 한 번은 Fresh로, 또 한 번은 Tree 또는 Cross로
각 정점은 리스트 Li에 한 번 삽입
그래프가 "인접리스트 구조"로 구현된 경우, BFS는 O(n + m) 시간에 수행된다

(추가)
*비트리(B-tree): 노드가 여러 키와 자식을 가질 수 있는 일반적인 균형 트리
AVL 트리와 같은 자가 균형 이진탐색트리로, 특히 대용량 데이터베이스와 파일 시스템에서 효율적인 디스크 I/O를 위해 설계되었다
비트리(B-tree) 간선
ㅇ후향간선 (v, w)

ㅇ교차간선 (v, w)

출처 및 참고: 알고리즘-원리와 응용(국형준교수님), Algorithm Design(Jon Kleinberg, Eva Tardos), Foundations of Algorithms using C++(Richard Neapolitan)
'Computer Science > 알고리즘' 카테고리의 다른 글
| [알고리즘] ep5-3) 방향그래프 (6) | 2024.07.23 |
|---|---|
| [알고리즘] ep5-2+) DFS, BFS 구현 (1) | 2024.07.22 |
| [알고리즘] ep5-1+) 인접리스트, 인접행렬 구현 (0) | 2024.07.21 |
| [알고리즘] ep5-1) 그래프(graph) (0) | 2024.07.21 |
| [알고리즘] ep4+++) 비활성화 방식 삭제 (0) | 2024.07.19 |



