[알고리즘] ep5-2+) DFS, BFS 구현

문제1) DFS 구현

입력으로 주어지는 그래프의 DFS 순회 결과를 출력하는 프로그램을 작성하시오.

입력 그래프의 성질:

n (1 ≤ n ≤ 100) 개의 정점과 m (1 ≤ m ≤ 1,000) 개의 간선으로 구성
정점은 1 ~ n 사이의 정수로 번호가 매겨져 있고, 정점의 번호는 모두 다름
모든 간선은 무방향 간선이고, 한 정점에서 임의의 다른 정점으로 가는 경로는 반드시 존재

구현 조건:

그래프는 인접리스트 구조를 사용하여 표현해야 한다.
인접 정점의 조사 순서: 정점 u의 인접 정점(or 부착 간선)들을 번호가 작은 정점부터 조사한다. (즉, 아래 DFS 의사 코드의 for 문에서 인접 정점들을 번호가 작은 정점부터 큰 순서대로 조사하라. 조사 순서에 따라 방문 결과가 달라질 수 있음에 유의할 것)

입력:

첫 줄에 정점의 개수 n, 간선의 개수 m, 순회 시작 정점 번호 s가 주어진다.
이후 m개의 줄에 한 줄에 하나씩 간선의 정보(간선의 양 끝 정점 번호)가 주어진다.
간선은 임의의 순서로 입력되고, 중복 입력되는 간선은 없다.
(무방향 간선이므로 간선 (u, v)와 (v, u)는 동일한 간선으로 취급)

출력:

출발정점 s에서 출발하는 DFS의 방문 순서대로 정점 번호를 출력한다.

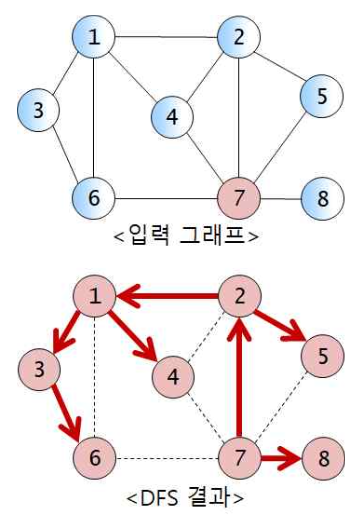
(전체코드)

// DFS: 인접리스트 - 연결리스트 (재귀)
#include <stdio.h>
#include <stdlib.h>

typedef struct INCIDENCE {
    int edgeIdx;
    struct INCIDENCE* next;
} INCIDENCE;

typedef struct VERTEX {
    int num;
    int label;
    INCIDENCE* incidence;
} VERTEX;

typedef struct EDGE {
    int u, v;
    int label;
} EDGE;

typedef struct GRAPH {
    VERTEX* vertex; // 정점 배열 (편의를 위해 index를 1부터 시작)
    EDGE* edge; // 간선 배열 (최대 간선 개수: 6 + 5 + 4 + 3 + 2 + 1 = 21)
    int vertexSize; // 정점의 수
    int curEdgeSize; // 현재 간선의 개수
} GRAPH;

GRAPH* graph;

void initGraph(int n, int m);
INCIDENCE* getIncidence(int edgeIdx);
void insertIncidence(int u, int v, INCIDENCE* incidence);
void insertEdge(int u, int v);
void DFS(int start);
void rDFS(int start);
void freeGraph();

int main() {
    int n, m, start;
    int u, v;

    scanf("%d %d %d", &n, &m, &start);
    initGraph(n, m);
    for (int i = 0; i < m; i++) {
        scanf("%d %d", &u, &v);
        insertEdge(u, v);
    }

    DFS(start);

    freeGraph();
    return 0;
}

void initGraph(int n, int m) {
    graph = (GRAPH*)malloc(1 * sizeof(GRAPH));
    graph->vertexSize = n;
    graph->curEdgeSize = 0;

     // 정점 배열을 1부터 사용하기 위해 n + 1크기로 할당
    graph->vertex = (VERTEX*)malloc((n + 1) * sizeof(VERTEX));
    graph->edge = (EDGE*)malloc(m * sizeof(EDGE));
    for (int i = 1; i <= graph->vertexSize; i++) {
        graph->vertex[i].incidence = NULL;
        graph->vertex[i].num = i;
    }
}

INCIDENCE* getIncidence(int edgeIdx) {
    INCIDENCE* node = (INCIDENCE*)malloc(1 * sizeof(INCIDENCE));
    node->next = NULL;
    node->edgeIdx = edgeIdx;
    return node;
}

void insertIncidence(int u, int v, INCIDENCE* incidence) {
    EDGE* edge = graph->edge;
    VERTEX* vertex = graph->vertex;
    INCIDENCE* ptr = vertex[u].incidence;
    if (ptr == NULL) { // 첫 노드
        vertex[u].incidence = incidence;
        return;
    }

    // 오름차순 삽입
    int other;
    if (edge[ptr->edgeIdx].u == u) {
        other = edge[ptr->edgeIdx].v;
    }
    else {
        other = edge[ptr->edgeIdx].u;
    }

    if (other > v) { // head에서 교환
        incidence->next = ptr;
        vertex[u].incidence = incidence;
        return;
    }
    while (ptr->next != NULL) {
        if (edge[ptr->next->edgeIdx].u == u) {
            other = edge[ptr->next->edgeIdx].v;
        }
        else {
            other = edge[ptr->next->edgeIdx].u;
        }

        if (other > v) {
            break;
        }
        ptr = ptr->next;
    }
    incidence->next = ptr->next;
    ptr->next = incidence;
}

void insertEdge(int u, int v) {
    EDGE* edge = graph->edge;

    // edge list에 중복 검사 및 추가
    for (int i = 0; i < graph->curEdgeSize; i++) {
        if (edge[i].u == u && edge[i].v == v ||
        edge[i].u == v && edge[i].v == u) {
            return;
        }
    }

    int cur = graph->curEdgeSize;

    edge[cur].u = u;
    edge[cur].v = v;

    // incidence node 생성 및 추가
    INCIDENCE* incidence1 = getIncidence(cur);
    INCIDENCE* incidence2 = getIncidence(cur);
    insertIncidence(u, v, incidence1);
    if (u != v) {
        insertIncidence(v, u, incidence2);
    }

    graph->curEdgeSize++;
}

void DFS(int start) {
    // 모든 정점을 방문하지 않은 상태로 초기화
    for (int i = 1; i <= graph->vertexSize; i++) {
        graph->vertex[i].label = 0;
    }
    // 모든 간선을 방문하지 않은 상태로 초기화
    for (int i = 0; i < graph->curEdgeSize; i++) {
        graph->edge[i].label = 0;
    }

    rDFS(start);
}

void rDFS(int cur) {
    EDGE* edge = graph->edge;
    graph->vertex[cur].label = 1; // 방문 표시
    printf("%d\n", cur); // 현재 정점 출력

    INCIDENCE* temp = graph->vertex[cur].incidence;
    int other;
    while (temp != NULL) {
        if (graph->edge[temp->edgeIdx].label == 0) { // 방문하지 않은 간선인 경우
            if (edge[temp->edgeIdx].u == graph->vertex[cur].num) {
                other = edge[temp->edgeIdx].v;
            }
            else {
                other = edge[temp->edgeIdx].u;
            }
            
            if (graph->vertex[other].label == 0) { // 방문하지 않은 정점인 경우
                graph->edge[temp->edgeIdx].label = 1; // 간선 방문 표시
                rDFS(other);
            }
        }
        temp = temp->next;
    }
}

void freeGraph() {
    for (int i = 1; i <= graph->vertexSize; i++) {
        INCIDENCE* cur = graph->vertex[i].incidence;
        while (cur != NULL) {
            INCIDENCE* temp = cur;
            cur = cur->next;
            free(temp);
        }
    }
    free(graph->vertex);
    free(graph->edge);
    free(graph);
}

/*
5 7 1
1 2
1 4
5 1
3 5
4 3
3 1
2 3

8 12 7
1 2
2 4
4 7
3 6
6 1
7 6
7 8
1 3
2 7
1 4
2 5
7 5
*/

문제2) BFS 구현

입력으로 주어지는 그래프의 BFS 순회 결과를 출력하는 프로그램을 작성하시오.

입력 그래프의 성질:

문제 1과 동일

구현 조건:

그래프는 인접행렬 구조를 사용하여 표현해야 한다.
인접 정점의 조사 순서: 문제 1과 동일하게 정점의 인접 정점(or 부착 간선)들을 번호가 작은 정점부터 조사한다.

입력: 문제 1과 동일

출력: 출발정점 s에서 출발하는 BFS의 방문 순서대로 정점 번호를 출력한다.

(전체코드)

// BFS: 인접행렬 - 배열
#include <stdio.h>
#include <stdlib.h>

typedef struct EDGE {
	int u, v;
	int label; // 1 or -1
} EDGE;

typedef struct VERTEX {
	int num;
	int label; // 1 or -1
} VERTEX;

typedef struct GRAPH {
	VERTEX* vertex;
	EDGE* edge;
	int** adjacency; // 인접행렬
	int vertexSize;
	int curEdgeSize;
} GRAPH;

GRAPH* graph;

void initGraph(int n, int m);
void insertEdge(int u, int v);
void BFS(int start);
void freeGraph(int n);

int main() {
	int n, m, start;
	int u, v;

	scanf("%d %d %d", &n, &m, &start);
	initGraph(n, m);
	for (int i = 0; i < m; i++) {
		scanf("%d %d", &u, &v);
		insertEdge(u, v);
	}

	BFS(start);

	return 0;
}

void initGraph(int n, int m) {
    graph = (GRAPH*)malloc(1 * sizeof(GRAPH));
	graph->vertexSize = n;
	graph->curEdgeSize = 0;

	graph->vertex = (VERTEX*)malloc(n * sizeof(VERTEX));
	graph->edge = (EDGE*)malloc(m * sizeof(EDGE));
	graph->adjacency = (int**)malloc(n * sizeof(int*));
	for (int i = 0; i < n; i++) {
		graph->adjacency[i] = (int*)malloc(n * sizeof(int));
	}

	for (int i = 0; i < n; i++) {
		graph->vertex[i].num = i + 1;
		graph->vertex[i].label = -1;
		for (int j = 0; j < n; j++) {
			graph->adjacency[i][j] = -1; // 가중치가 0일 수 있으니 -1로 초기화
		}
	}
	for (int i = 0; i < m; i++) {
		graph->edge[i].label = -1;
	}
}

void insertEdge(int u, int v) {
	// edge list에 중복 검사 및 추가
	EDGE* edge = graph->edge;
	for (int i = 0; i < graph->curEdgeSize; i++) {
		if (edge[i].u == u && edge[i].v == v
            || edge[i].u == v && edge[i].v == u) {
            return;
		}
	}

	int idx = graph->curEdgeSize;
	edge[idx].u = u;
	edge[idx].v = v;
	edge[idx].label = 1;

	// 인접행렬 (무방향 그래프이므로 배열 양쪽에 추가)
	graph->adjacency[u - 1][v - 1] = idx;
	graph->adjacency[v - 1][u - 1] = idx;

	graph->curEdgeSize++;
}

void BFS(int start) {
    int front = 0, rear = 0;
    int* queue = (int*)malloc(graph->vertexSize * sizeof(int));
    queue[rear++] = start;
    graph->vertex[start - 1].label = 1;

    printf("%d\n", start);
    while (front < rear) { // 큐가 빌 때까지 반복
        int cur = queue[front++]; // 현재 방문할 정점을 큐에서 꺼낸다
        for (int i = 0; i < graph->vertexSize; i++) {
            if (graph->adjacency[cur - 1][i] != -1 && graph->vertex[i].label == -1) {
				// 인접행렬에 체크가 되어있고 방문라벨이 안되어 있으면 출력
                printf("%d\n", graph->vertex[i].num);

                graph->vertex[i].label = 1;
                queue[rear++] = graph->vertex[i].num;
            }
        }
    }

    free(queue);
}

void freeGraph(int n) {
    for (int i = 0; i < n; i++) {
        free(graph->adjacency[i]);
    }
    free(graph->adjacency);
    free(graph->vertex);
    free(graph->edge);
    free(graph);
}

/*
6 9 1
3 5
1 3
4 1
2 3
3 4
6 4
3 6
1 2
2 5

8 12 4
1 2
2 4
4 7
3 6
6 1
7 6
7 8
1 3
2 7
1 4
2 5
7 5
*/

출처 및 참고: 알고리즘-원리와 응용(국형준교수님), Algorithm Design(Jon Kleinberg, Eva Tardos), Foundations of Algorithms using C++(Richard Neapolitan)

저작자표시 비영리 변경금지

'Computer Science > 알고리즘' 카테고리의 다른 글

[알고리즘] ep5-3+) 위상순서 찾기 (7)	2024.07.24
[알고리즘] ep5-3) 방향그래프 (6)	2024.07.23
[알고리즘] ep5-2) 그래프 순회 (0)	2024.07.21
[알고리즘] ep5-1+) 인접리스트, 인접행렬 구현 (0)	2024.07.21
[알고리즘] ep5-1) 그래프(graph) (0)	2024.07.21