[자료구조] ep8) 분리집합(Disjoint Set)

ㅇ분리집합 ADT: 교집합이 없는 집합들

서로소집합이라고도 불리며 Union-Find라고도 한다

e.g. 혈액형 집합

 

소속 관계가 분명해야 하는 데이터를 다룰 때 유용하다

목적: 원소가 어느 집합에 귀속되어 있는지 (find 함수)

 

직접 응용: 동치관계(e.g. 그래프), 최소신장트리

간접 응용: 알고리즘 구현, 저료구조 구현

 

 

<주요 메서드>

- set find(e): 원소 e가 속한 집합을 반환

- union(x, y): 집합 x, y를 통합

<보조 메서드>

- int size(S): 집합 S 원소의 수를 반환

 

 

[구현 방법 2가지]

1. 리스트(or 배열)에 기초한 구현 

find는 빠르고 union은 느리다

2. 트리에 기초한 구현

find는 느리고 union은 빠르다

 

A, B, C 분리집합 sample

 

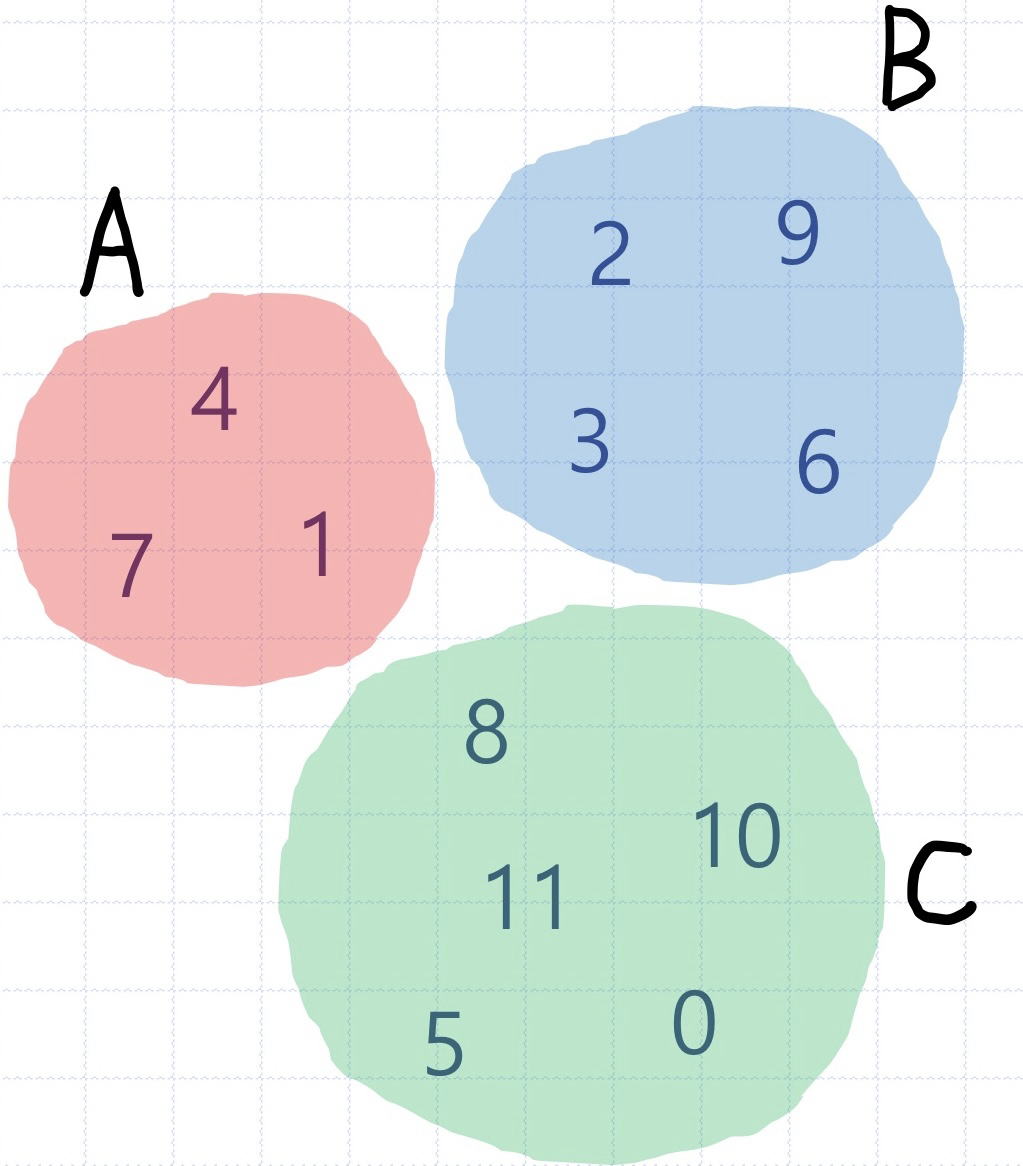
1-1 리스트에 기초한 구현: 분리집합 집단을 레코드의 배열로 표현

한 개의 분리집합에 대해 단일연결리스트를 사용

 

 

1-2 배열에 기초한 구현: 소속집합을 원소값으로 하는 크기 n의 배열 S로 분리집합을 표현

 

 

 

 

2. 트리에 기초한 구현: 연결트리 + 가상트리로 구현

기본적으로 자식이 부모를 가리키는 구조이며, 각 집합은 트리의 루트로 식별한다

한 개의 분리집합에 대해 한 개의 트리를 사용

 

- 연결트리: 각 노드는 원소 및 부모를 가리키는 포인터를 저장 (단, 루트 노드는 자신을 부모로 하는 포인터를 저장)

- 가상트리: 자식을 가리키는 포인터가 불필요하므로, 트리 ADT 대신에 배열에 의한 가상트리로 구현하면 충분 - Parent 배열

 

Parent 배열

 

 

 

union 함수 모식도)

트리 x, y 중 하나를 다른 트리의 부트리로 만든다

 

 

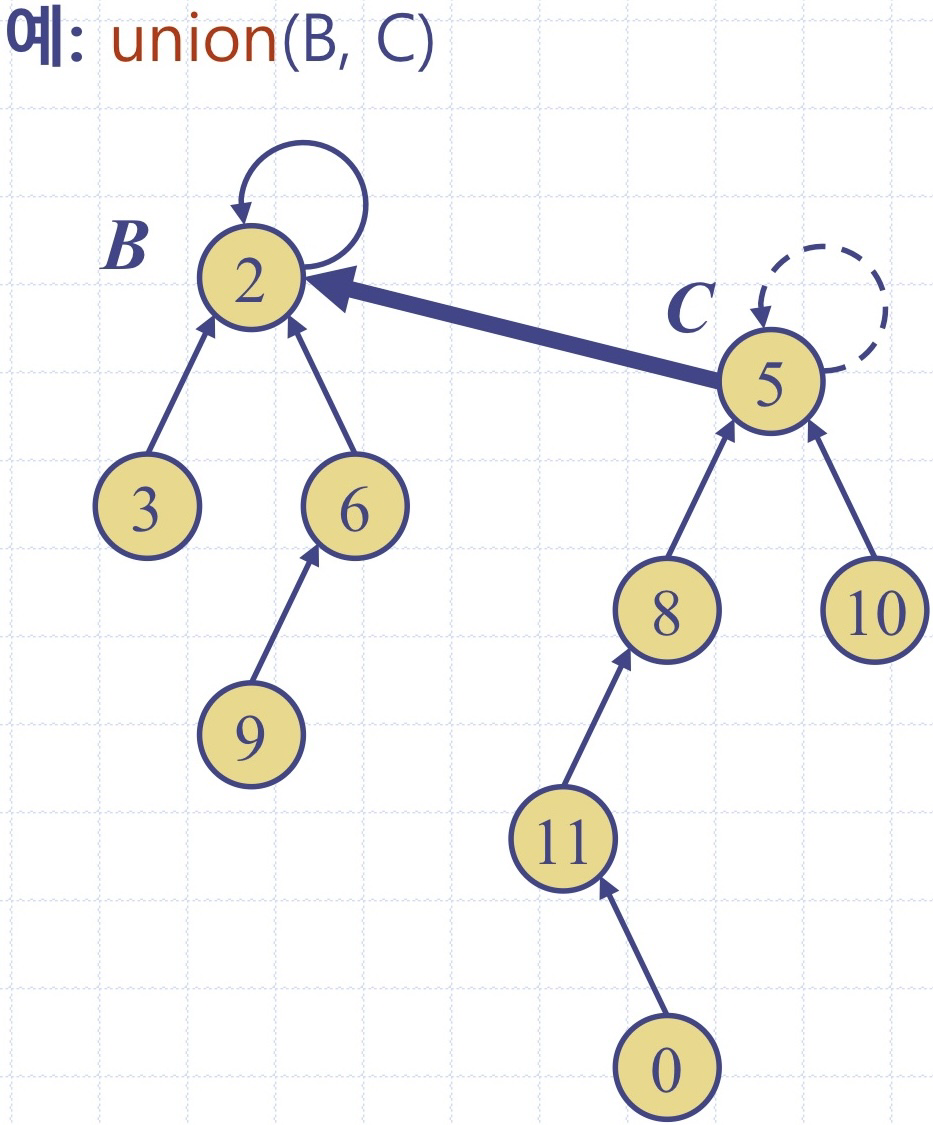
find 함수 모식도)

e의 부모포인터를 따라 루트까지 올라간다

 

 

 

 

 

 

 

 

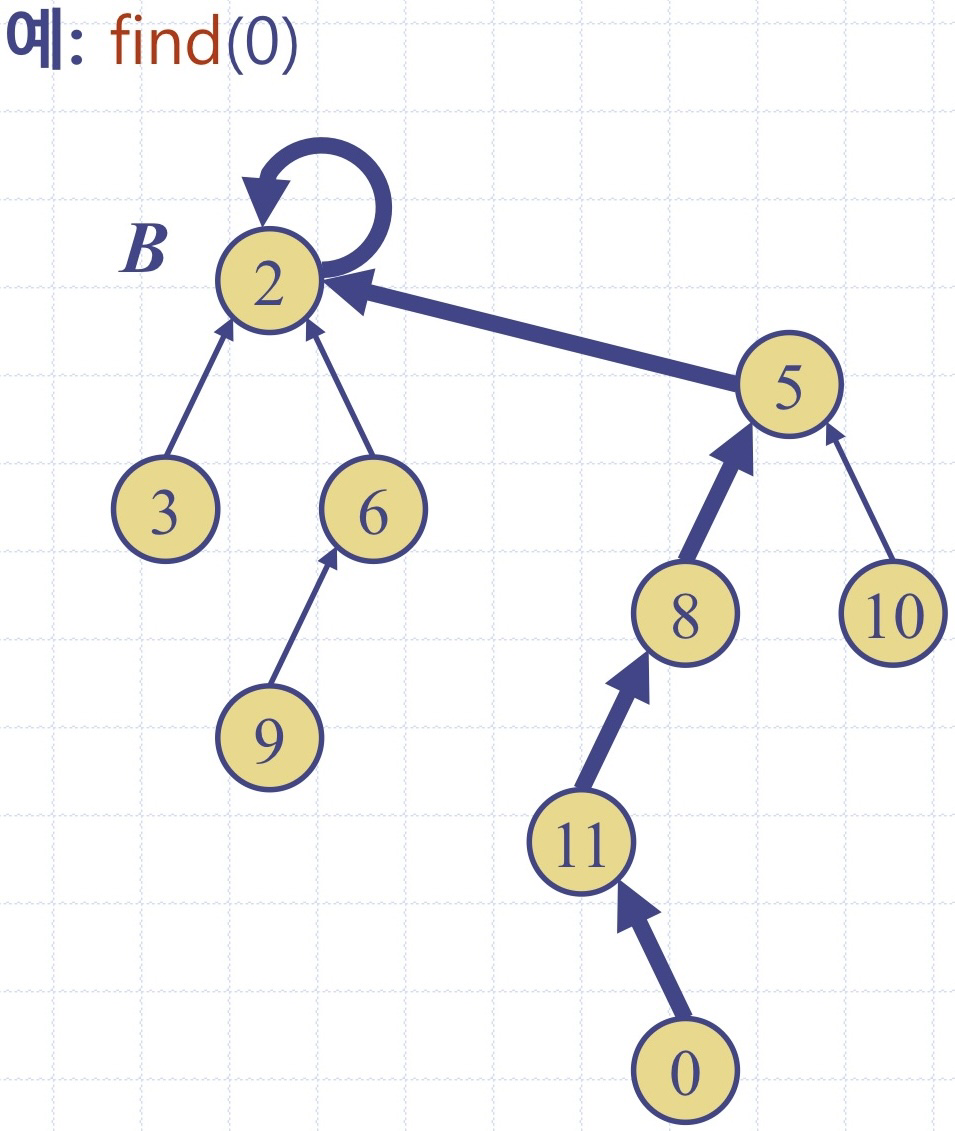
참고 및 출처: 데이터 구조 원리와 응용(국형준교수님), C언어로 쉽게 풀어 쓴 자료구조(천인국)