[ps java] binarySearch() 정석 코드 2가지 버전

https://claremont.tistory.com/entry/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-ep2-%EC%82%AC%EC%A0%84dictionary

[알고리즘] ep2) 사전(dictionary)

(이진탐색은 자료가 순서에 따라 정렬되어있어야 할 수 있다)

 

 

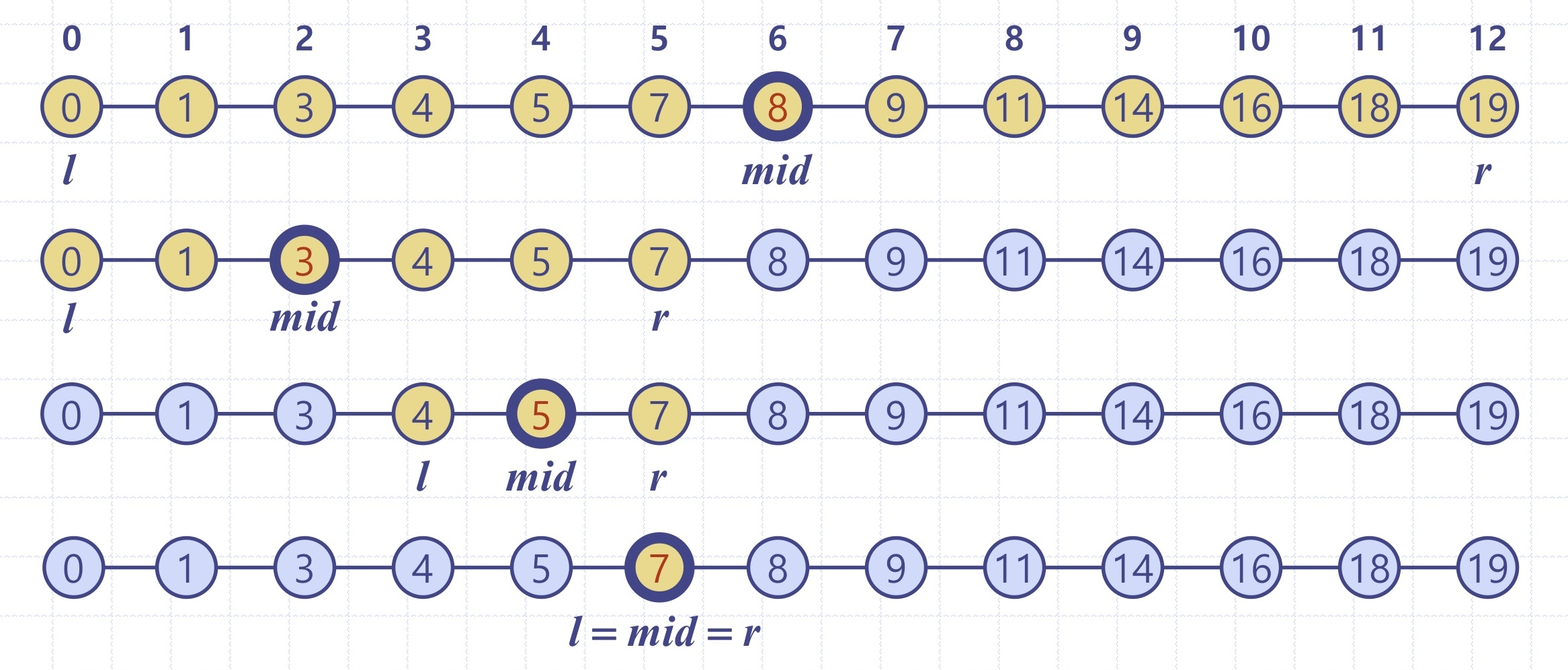
1. 반복문 버전: 디버깅에도 용이하고 메모리도 덜 잡아먹으므로 재귀방식보다 더 추천한다

import java.io.*;
import java.util.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        
        int N = Integer.parseInt(br.readLine());
        int[] arr = new int[N];
        
        .
        .
        .
        .
        .
        .
        .
        .
        .
        .
        .
        .
        .
        .
        .
        .
        .
        .
        .
        .
        
        br.close();
    }

    public static int binarySearch(int[] arr, int key) {
        int lowIdx = 0;
        int highIdx = arr.length - 1;

        while (lowIdx <= highIdx) {
            int midIdx = (highIdx - lowIdx) / 2 + lowIdx;

            if (arr[midIdx] < key) {
                lowIdx = midIdx + 1;
            } else if (arr[midIdx] > key) {
                highIdx = midIdx - 1;
            } else {
                return midIdx;
            }
        }

        return -1;
    }
}

 

 

 

2. 재귀 버전: 디버깅에 용이하지 않고 메모리(스택 메모리)를 더 사용하게 되므로 추천하지는 않는다

import java.io.*;
import java.util.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        
        .
        .
        .
        .
        .
        .
        .
        .
        .
        .
        .
        .
        .
        .
        .
        .
        .
        .
        .
        .

        br.close();
    }

    public static int binarySearch(int[] arr, int key, int lowIdx, int highIdx) {
        if (lowIdx > highIdx) {
            return -1;
        }

        int midIdx = (highIdx - lowIdx) / 2 + lowIdx;

        if (arr[midIdx] < key) {
            return binarySearch(key, midIdx + 1, highIdx);
        } else if (arr[midIdx] > key) {
            return binarySearch(key, lowIdx, midIdx - 1);
        } else {
            return midIdx;
        }
    }
}

 

 

 

 

(참고)

Arrays.binarySearch()는 Array 전용 이진 탐색 메서드이고

Collections.binarySearch()는 List 전용 이진 탐색 메서드이다!