"컴퓨터는 0과 1밖에 이해하지 못한다"
ㅇ비트(bit): 0과 1을 나타내는 가장 작은 정보 단위
따라서 한 비트는 두 가지 정보만을(0 or 1) 표현한다

한 비트는 두 가지 경우의 수(0 or 1)만을 가지므로
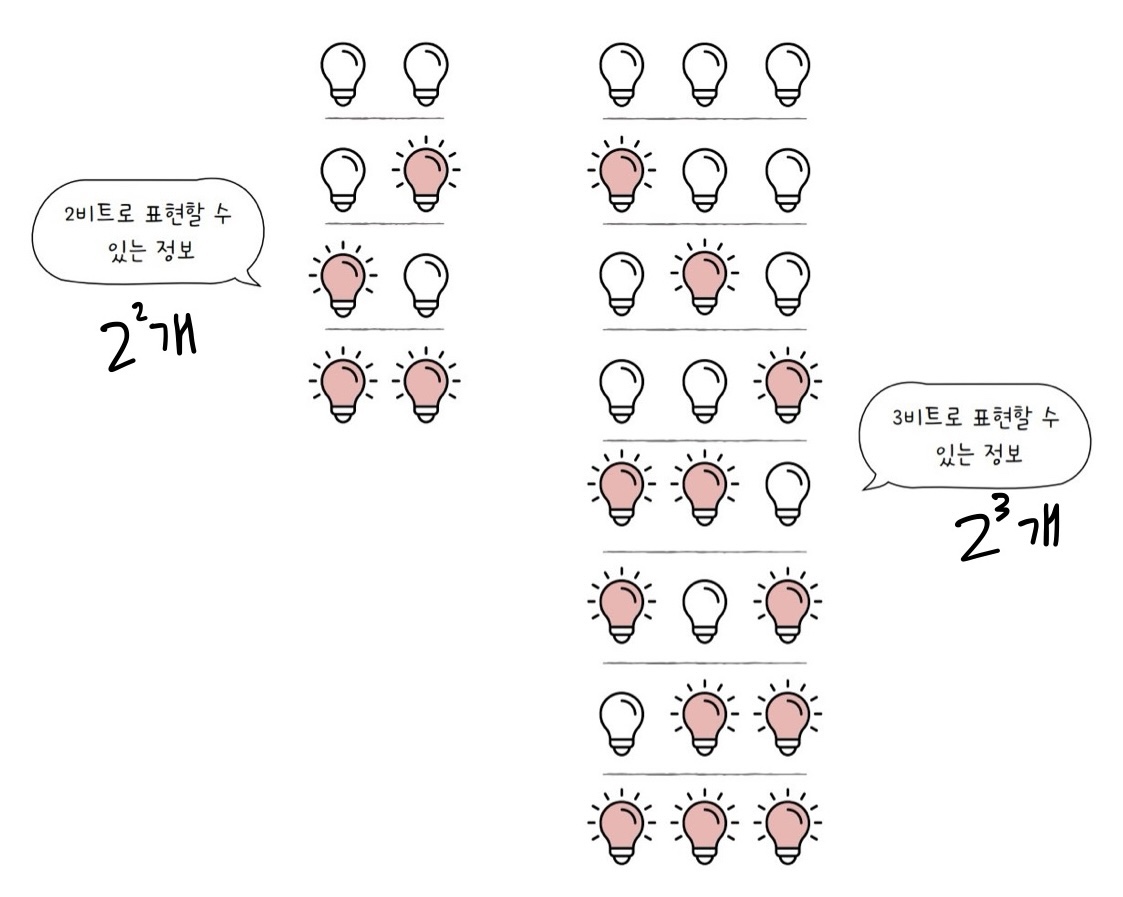
2비트로 표현할 수 있는 정보의 개수는 2^2개
3비트로 표현할 수 있는 정보의 개수는 2^3개
.
.
.
n비트로 표현할 수 있는 정보의 개수는 2^n개
여기서 1byte는 8개의 bit를 뜻한다 (1byte = 8bit)
10^3byte = 1kB [킬로바이트]
10^6byte = 1MB [메가바이트]
10^9byte = 1GB [기가바이트]
10^12byte = 1TB [테라바이트]
10^15byte = 1PB [페타바이트]
ㅇ워드(word): CPU가 한 번에 처리할 수 있는 데이터 크기
하프 워드(half word): 워드의 절반 크기
풀 워드(full word): 워드의 1배 크기
더블 워드(double word): 워드의 2배 크기
현대 컴퓨터의 워드 크기는 대부분 32비트 또는 64비트이다
e.g. x86 CPU: 32bit
x64 CPU: 64bit
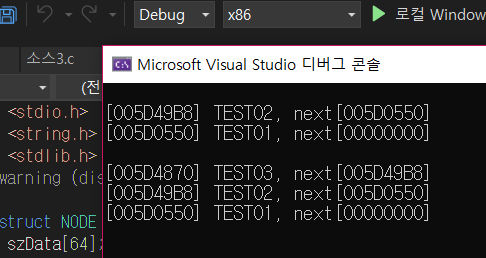
(Visual Studio 상단에서 솔루션 플랫폼을 x86(32bit)로 설정하면 출력되는 주소의 길이가 짧고
솔루션 플랫폼을 x64(64bit)로 설정하면 출력되는 주소의 길이가 긴 것을 알 수가 있다)
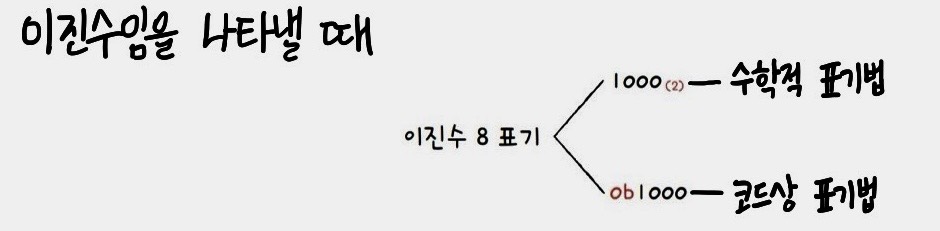
ㅇ이진수(binary)
8을 이진수로 나타낼 때
2의 보수: 이진수의 음수표현 방법
그냥 다 뒤집고 마지막에 1을 더하면 된다

하지만 2의 보수 방법에는 0과 2^n의 경우 오류가 발생한다(그림참고)
따라서 컴퓨터는 CPU 내부의 레지스터 flag를 이용한다

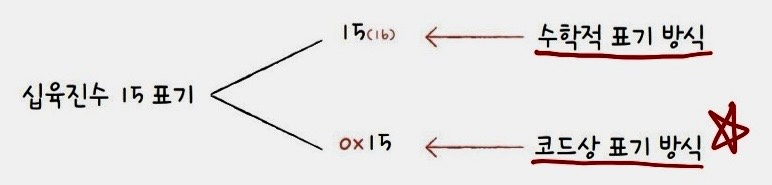
ㅇ십육진법(hexadecimal)
15를 십육진수로 나타낼 때
+ 십육진수를 세는 꿀팁: "주먹을 쥐었을 때가 A(10)"

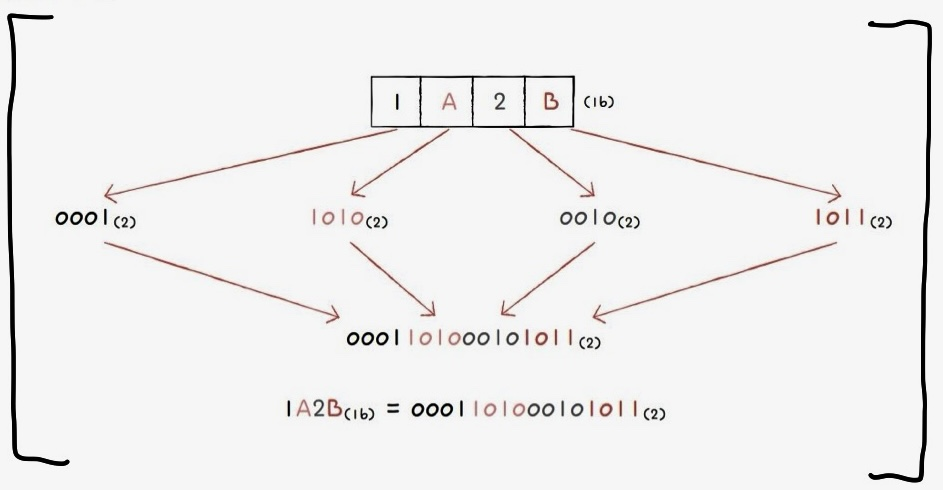
왜 컴퓨터는 복잡한 십육진수를 채택한 것일까?
그 이유는 십육진수->이진수, 이진수->십육진수로의 변환이 편리하여서이다
ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ
인코딩: 컴퓨터가 알 수 있게 0과 1로 변환(코드화)
디코딩: 0과 1을 사람이 알 수 있게 변환
아스키코드: 초창기 문자집합 ('A'의 코드 포인트는 65)
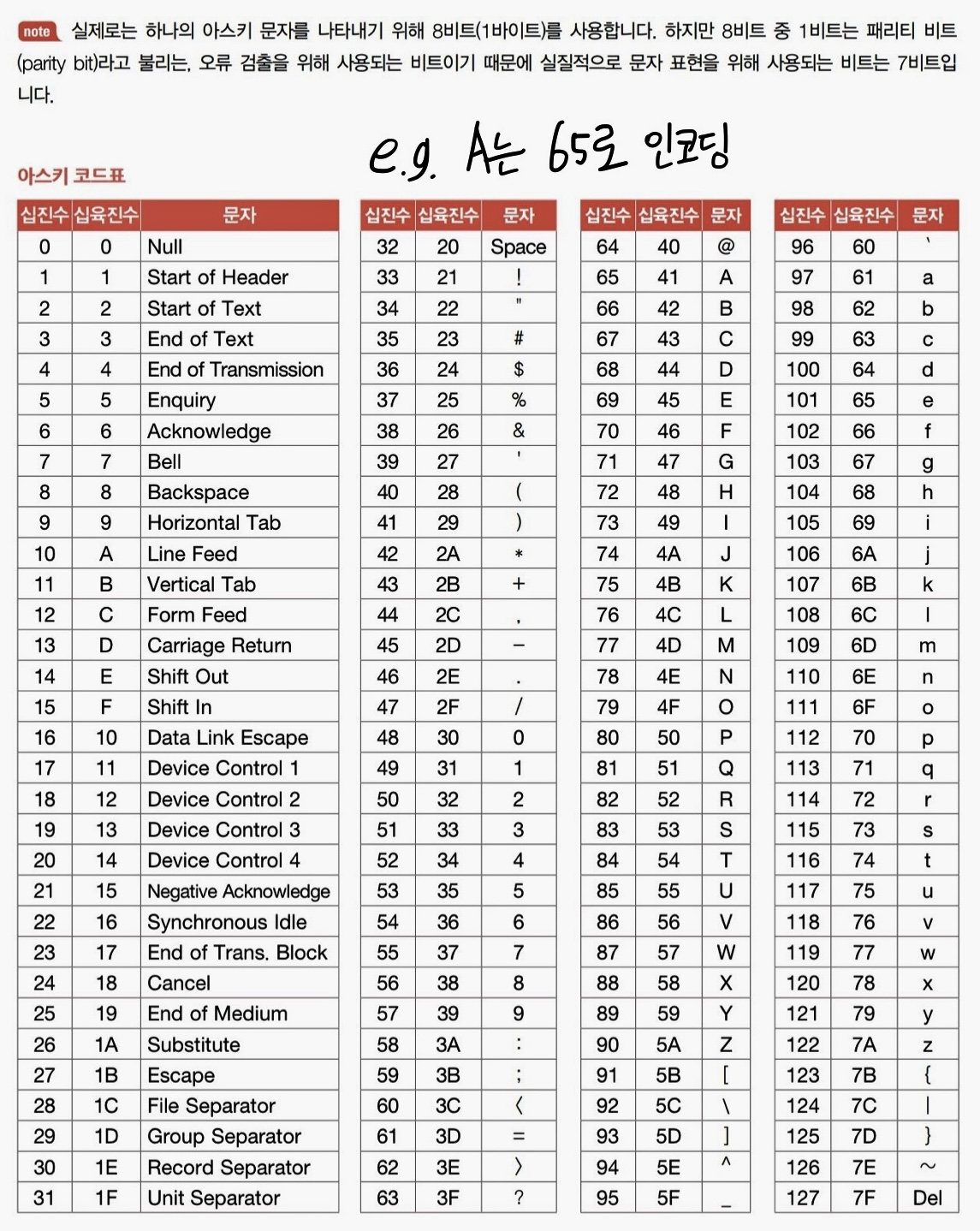
하지만 이걸로는 턱없이 부족해서 나온 것이
확장아스키! 하지만 이걸로도 턱없이 부족했다
※우리나라는 한글 인코딩을 위하여 EUC-KR을 사용하였고 그에 대한 확장판으로 CP949가 나왔지만 이마저도 한글 전체를 표현하기에 넉넉한 양은 아니었다
각 나라의 인코딩 방식이 달라 매우 복잡했다
그리고 이것을 해결하기 위해 하나의 통일된 국제 문자 코드 규약이 나오게 되었다
그것이 바로 유니코드(UTF-8)이다
(여기서 UTF란 Unicode Transformation Format의 약자로 전문적 지식을 요하지 않는 분야에서 그냥 유니코드라고 했을 때는 십중팔구 이 인코딩이라 생각하면 될 정도로 표준적인, 호환성이 가장 좋은 인코딩이다)
참고 및 출처: 컴퓨터시스템구조론(William Stallings), 혼공컴운(강민철)
'Computer Science > 컴퓨터 구조' 카테고리의 다른 글
| [컴퓨터 구조] ep6) 메모리와 캐시메모리 (0) | 2024.02.19 |
|---|---|
| [컴퓨터 구조] ep5) CPU 성능 향상 기법 (0) | 2024.02.14 |
| [컴퓨터 구조] ep4) CPU와 인터럽트 (2) | 2024.02.14 |
| [컴퓨터 구조] ep2) 명령어와 주소 지정 방식 (2) | 2024.02.11 |
| [컴퓨터 구조] ep0) 컴퓨터 구조가 중요한 이유 (0) | 2024.01.17 |



