주의: 그래프 알고리즘 구현 시, 그래프의 인접 정보(즉, 부착 간선리스트 또는 인접행렬) 없이도 수행 가능한 문제라고 판단되면 간선리스트 구조로 그래프를 간편하게 구현할 것을 우선적으로 고려하라. 그렇지 않고, 인접 정보가 있어야 수행한다고 판단되면 인접리스트 구조 또는 인접행렬 구조 중에 해당 문제 해결에 효율성 면에서 유리하다고 판단되는 것을 선택하여 구현하라.
문제1) Prim-Jarnik 알고리즘 구현
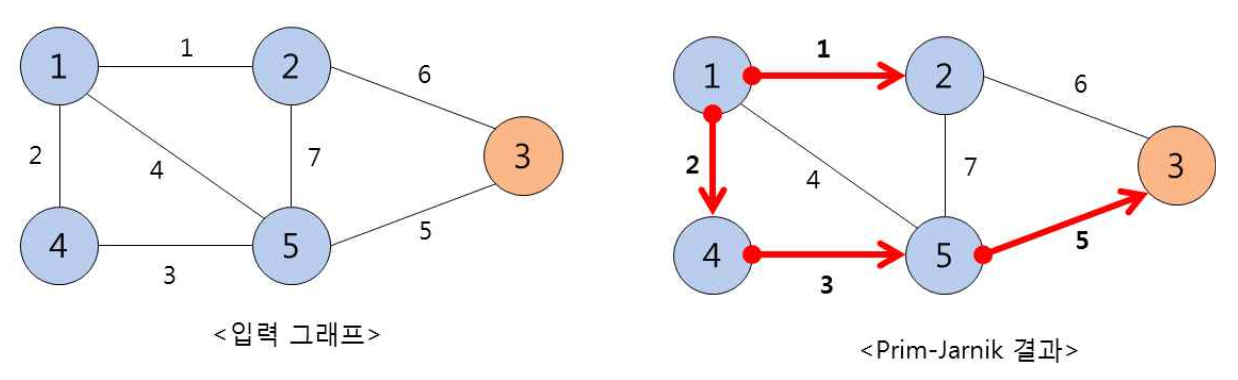
입력으로 주어지는 그래프를 Prim-Jarnik 알고리즘을 이용하여 최소신장트리(Minimum Spanning Tree, MST)를 생성하는 프로그램을 작성하고, 최소신장트리의 생성 과정과 총무게를 결과로 출력하시오.
입력 그래프의 성질:
- n (1 ≤ n ≤ 100) 개의 정점과 m (1 ≤ m ≤ 1,000) 개의 간선으로 구성된다.
- 정점은 1 ~ n 사이의 정수로 번호가 매겨져 있고, 정점의 번호는 모두 다르다.
- 모든 간선은 무방향간선이고, 한 정점에서 임의의 다른 정점으로 가는 경로는 반드시 존재한다.
- 간선의 무게는 중복이 없는 양의 정수다.
(알고리즘 수행의 출발정점은 번호가 가장 빠른 정점인 1부터 시작하며, Prim-Jarnik 알고리즘의 첫 출발 정점은 그래프 내 아무 정점이라도 무방하지만, 이 문제에서는 번호가 가장 빠른 정점인 1에서 출발한다 가정한다)
◦ 입력
- 첫 줄에 정점의 개수 n, 간선의 개수 m이 주어진다.
- 이후 m개의 줄에 한 줄에 하나씩 간선의 정보(간선의 양끝 정점 번호와 무게)가 주어진다. 간선은 임의의 순서로 입력되고, 중복 입력되는 간선은 없다. (무방향간선이므로 간선 (u, v)와 (v, u)는 동일한 간선으로 취급)
- 무게로는 양의 정수가 입력되고, 중복되는 무게는 없다.
◦ 출력
- 모든 정점의 번호를 출력한 후, 마지막 줄에 MST 간선 무게의 합 즉, 총무게를 출력한다.

(전체코드)
// Prim-Jarnik 알고리즘 by 우선순위 큐(최소 힙)
#include <stdio.h>
#include <stdlib.h>
// 간선의 인접 정보를 나타내는 노드 구조체
typedef struct INCIDENT {
int edgeIdx;
struct INCIDENT* next;
} INCIDENT;
typedef struct VERTEX {
int num;
int minDistance;
INCIDENT* head; // 인접 리스트의 헤드
} VERTEX;
typedef struct EDGE {
int u, v;
int w;
} EDGE;
typedef struct GRAPH {
int n, m;
VERTEX* vertex;
EDGE* edge;
} GRAPH;
typedef struct HEAP {
int num; // 정점 번호 (key)
int distance; // 정점까지의 거리 값 (e)
} HEAP;
GRAPH graph;
void initGraph(int n, int m);
void insertVertex(int idx);
void insertIncidentEdge(int u, int v, int w, int idx);
void addIncidentNode(INCIDENT* head, int idx);
void freeGraph();
void PrimJarnikMST();
HEAP* buildMinHeap();
void upHeap(HEAP* heap, int idx);
void downHeap(HEAP* heap, int idx, int heapSize);
int extractMin(HEAP* heap, int heapSize);
void updateKey(HEAP* heap, int heapSize, int v, int newDistance);
void swapElem(HEAP* x, HEAP* y);
int getOppositeVertex(int u, int edgeIdx);
int isVertexInHeap(HEAP* heap, int heapSize, int v);
int main(void) {
int n, m; // 정점 수, 간선 수
int u, v, w;
scanf("%d %d", &n, &m);
initGraph(n, m);
for (int i = 0; i < graph.m; i++) {
scanf("%d %d %d", &u, &v, &w);
insertIncidentEdge(u, v, w, i); // 간선 정보 삽입
}
PrimJarnikMST();
freeGraph();
return 0;
}
void initGraph(int n, int m) {
graph.vertex = (VERTEX*)malloc((n + 1) * sizeof(VERTEX)); // 정점 번호는 1부터 시작
graph.edge = (EDGE*)malloc(m * sizeof(EDGE));
graph.n = n;
graph.m = m;
for (int i = 1; i <= n; i++) {
graph.vertex[i].num = i;
graph.vertex[i].head = (INCIDENT*)malloc(1 * sizeof(INCIDENT));
graph.vertex[i].head->next = NULL;
}
}
void insertIncidentEdge(int u, int v, int w, int idx) {
graph.edge[idx].u = u;
graph.edge[idx].v = v;
graph.edge[idx].w = w;
// 간선을 각 정점의 incident 리스트에 추가
addIncidentNode(graph.vertex[u].head, idx);
addIncidentNode(graph.vertex[v].head, idx);
}
void addIncidentNode(INCIDENT* head, int idx) {
INCIDENT* node = (INCIDENT*)malloc(1 * sizeof(INCIDENT));
node->edgeIdx = idx; // 간선 인덱스 설정
node->next = head->next; // 인접 리스트에 삽입
head->next = node; // 인접 리스트 업데이트
}
void freeGraph() {
INCIDENT* cur;
for (int i = 1; i <= graph.n; i++) {
cur = graph.vertex[i].head; // 인접 리스트의 헤드
while (cur != NULL) {
INCIDENT* temp = cur;
free(temp);
cur = cur->next;
}
}
free(graph.vertex);
free(graph.edge);
}
void PrimJarnikMST() {
for (int i = 1; i <= graph.n; i++) { // 초기화
graph.vertex[i].minDistance = 2147483647;
}
graph.vertex[1].minDistance = 0; // 시작 정점의 거리 값은 0
HEAP* heap = buildMinHeap();
INCIDENT* ptr;
int u, v;
int distanceSum = 0; // MST 가중치 합
int heapSize = graph.n;
while (heapSize > 0) {
u = extractMin(heap, heapSize); // 최소 거리 정점 추출
printf(" %d", graph.vertex[u].num);
distanceSum += graph.vertex[u].minDistance;
ptr = graph.vertex[u].head->next; // 인접 리스트 순회 시작
while (ptr != NULL) {
v = getOppositeVertex(u, ptr->edgeIdx); // 간선의 반대쪽 정점 찾기
if (isVertexInHeap(heap, heapSize, v) && graph.edge[ptr->edgeIdx].w < graph.vertex[v].minDistance) {
// 간선의 가중치가 더 작으면 거리 값 갱신
graph.vertex[v].minDistance = graph.edge[ptr->edgeIdx].w;
updateKey(heap, heapSize, v, graph.vertex[v].minDistance); // 힙에서 거리 값 갱신
}
ptr = ptr->next;
}
heapSize--;
}
printf("\n");
printf("%d", distanceSum);
free(heap);
}
HEAP* buildMinHeap() {
HEAP* heap = (HEAP*)malloc((graph.n + 1) * sizeof(HEAP));
// 초기화
for (int i = 1; i <= graph.n; i++) {
heap[i].distance = graph.vertex[i].minDistance; // 정점의 최소 거리 값 저장
heap[i].num = graph.vertex[i].num; // 정점 번호 저장
}
for (int i = graph.n / 2; i >= 1; i--) { // 상향식 힙생성
downHeap(heap, i, graph.n);
}
return heap;
}
void upHeap(HEAP* heap, int idx) {
if (idx == 1) {
return;
}
if (heap[idx].distance >= heap[idx / 2].distance) { // 부모 노드보다 크거나 같으면 종료
return;
}
swapElem(heap + idx, heap + idx / 2); // 부모 노드와 교환
upHeap(heap, idx / 2); // 부모 노드로 올라감
}
void downHeap(HEAP* heap, int idx, int heapSize) {
int leftChildIdx = 2 * idx;
int rightChildIdx = 2 * idx + 1;
int smaller;
if (leftChildIdx > heapSize) {
return;
}
smaller = leftChildIdx;
if (rightChildIdx <= heapSize) {
if (heap[rightChildIdx].distance < heap[leftChildIdx].distance) {
smaller = rightChildIdx;
}
}
if (heap[idx].distance <= heap[smaller].distance) {
return;
}
swapElem(heap + idx, heap + smaller); // 부모 노드와 더 작은 자식 노드 교환
downHeap(heap, smaller, heapSize); // 자식 노드로 내려감
}
// 힙에서 최소 가중치 간선 추출 함수
int extractMin(HEAP* heap, int heapSize) {
if (heapSize == 0) {
return -1;
}
HEAP res = heap[1]; // 루트 노드 추출
swapElem(heap + 1, heap + heapSize); // 루트 노드와 마지막 노드 교환
downHeap(heap, 1, heapSize - 1);
return res.num;
}
// 힙에서 키 값 교체
void updateKey(HEAP* heap, int heapSize, int v, int newDistance) {
int i;
for (i = 1; i < heapSize; i++) { // 힙 내 정점 검색
if (heap[i].num == v) {
heap[i].distance = newDistance;
break;
}
}
upHeap(heap, i);
}
void swapElem(HEAP* x, HEAP* y) {
HEAP temp;
temp = *x;
*x = *y;
*y = temp;
}
// 간선의 반대쪽 정점 반환
int getOppositeVertex(int u, int edgeIdx) {
return (graph.edge[edgeIdx].u == u) ? graph.edge[edgeIdx].v : graph.edge[edgeIdx].u;
}
// 힙에 정점이 포함되어 있는지 확인
int isVertexInHeap(HEAP* heap, int heapSize, int v) {
for (int i = 1; i < heapSize; i++) { // 힙 내 정점 검색
if (heap[i].num == v)
return 1;
}
return 0;
}
/*
5 7
1 2 1
1 4 2
1 5 4
2 5 7
4 5 3
3 5 5
2 3 6
*/
문제2) Kruskal 알고리즘 구현
입력으로 주어지는 그래프를 Kruskal 알고리즘을 이용하여 최소신장트리(Minimum Spanning Tree, MST)를 생성하는 프로그램을 작성하고, 최소신장트리의 생성 과정과 총무게를 결과로 출력하시오.
입력 그래프의 성질은 문제 1의 입력 그래프 성질과 동일하다.
(Kruskal 알고리즘 구현 시, 우선순위 큐와 분리집합의 구현이 필요할 수 있다.)
◦ 입력
- 문제 1의 입력과 동일하다.
◦ 출력
- 최소신장트리(MST) 생성 과정에서 추가되는 간선의 무게를 순서대로 출력한다.
- 모든 간선의 무게를 출력한 후, 마지막 줄에 MST 간선 비용의 합 즉, 총무게를 출력한다.




(전체코드)
// Kruskal 알고리즘 by 우선순위 큐(최소 힙) + 분리집합
#include <stdio.h>
#include <stdlib.h>
// 간선의 인접 정보를 나타내는 노드 구조체
typedef struct INCIDENT {
int edgeIdx;
struct INCIDENT* next;
}INCIDENT;
typedef struct VERTEX {
int num;
} VERTEX;
typedef struct EDGE {
int u, v;
int w;
} EDGE;
typedef struct GRAPH {
int n, m;
VERTEX* vertex;
EDGE* edge;
} GRAPH;
// 서로소 집합을 나타내는 구조체
typedef struct DISJOINTSET {
int setSize;
INCIDENT* head; // 인접 리스트의 헤드
} DISJOINTSET;
typedef struct HEAP {
int edgeIdx; // key
int w; // e
} HEAP;
GRAPH graph;
void initGraph(int n, int m);
void insertIncidentEdge(int u, int v, int w, int idx);
void addIncidentNode(INCIDENT** head, int idx);
int removeIncidentNode(INCIDENT** head);
void freeGraph();
void KruskalMST();
DISJOINTSET* buildDisjointSet();
HEAP* buildMinHeap();
void downHeap(HEAP* heap, int idx, int heapSize);
int extractMin(HEAP* heap, int heapSize);
int findSet(DISJOINTSET* set, int v);
void unionSet(DISJOINTSET* set, int u, int v);
void swapElem(HEAP* x, HEAP* y);
void freeSet(DISJOINTSET* set);
int main(void) {
int n, m;
int u, v, w;
scanf("%d %d", &n, &m);
initGraph(n, m);
for (int i = 0; i < graph.m; i++) {
scanf("%d %d %d", &u, &v, &w);
insertIncidentEdge(u, v, w, i);
}
KruskalMST();
freeGraph();
return 0;
}
void initGraph(int n, int m) {
graph.vertex = (VERTEX*)malloc((n + 1) * sizeof(VERTEX)); // 정점 번호는 1부터 시작
graph.edge = (EDGE*)malloc(m * sizeof(EDGE));
graph.n = n;
graph.m = m;
for (int i = 1; i <= n; i++) {
graph.vertex[i].num = i;
}
}
void insertIncidentEdge(int u, int v, int w, int idx) {
graph.edge[idx].u = u;
graph.edge[idx].v = v;
graph.edge[idx].w = w;
}
void addIncidentNode(INCIDENT** head, int idx) {
INCIDENT* node = (INCIDENT*)malloc(1 * sizeof(INCIDENT));
node->edgeIdx = idx; // 간선 인덱스 설정
node->next = *head; // 새 노드를 헤드에 연결
*head = node; // 헤드를 새 노드로 변경
}
int removeIncidentNode(INCIDENT** head) {
if (*head == NULL) {
return -1;
}
int idxToRemove = (*head)->edgeIdx;
*head = (*head)->next; // 헤드를 다음 노드로 변경
return idxToRemove;
}
void freeGraph() {
free(graph.vertex);
free(graph.edge);
}
void KruskalMST() {
DISJOINTSET* set = buildDisjointSet();
HEAP* heap = buildMinHeap();
int heapSize = graph.m;
int distanceSum = 0; // MST 가중치 합
int minEdgeIdx, u, v;
while (heapSize > 0) {
minEdgeIdx = extractMin(heap, heapSize); // 최소 가중치 간선 추출
u = findSet(set, graph.edge[minEdgeIdx - 1].u); // 간선의 시작 정점의 집합 찾기
v = findSet(set, graph.edge[minEdgeIdx - 1].v); // 간선의 끝 정점의 집합 찾기
if (u != v) { // 두 정점이 다른 집합에 속해 있다면
printf(" %d", graph.edge[minEdgeIdx - 1].w);
distanceSum += graph.edge[minEdgeIdx - 1].w;
unionSet(set, u, v); // 두 집합 합치기
}
heapSize--;
}
printf("\n");
printf("%d", distanceSum);
freeSet(set);
free(heap);
}
// 서로소 집합 생성 함수
DISJOINTSET* buildDisjointSet() {
DISJOINTSET* set = (DISJOINTSET*)malloc(graph.n * sizeof(DISJOINTSET));
for (int i = 0; i < graph.n; i++) {
set[i].setSize = 0;
set[i].head = (INCIDENT*)malloc(1 * sizeof(INCIDENT));
set[i].head->edgeIdx = graph.vertex[i + 1].num;
set[i].head->next = NULL;
}
return set;
}
HEAP* buildMinHeap() {
HEAP* heap = (HEAP*)malloc((graph.m + 1) * sizeof(HEAP));
for (int i = 1; i <= graph.m; i++) { // 초기화
heap[i].w = graph.edge[i - 1].w;
heap[i].edgeIdx = i;
}
for (int i = graph.m / 2; i >= 1; i--) { // 상향식 힙생성
downHeap(heap, i, graph.m);
}
return heap;
}
void downHeap(HEAP* heap, int idx, int heapSize) {
int leftChildIdx = 2 * idx;
int rightChildIdx = 2 * idx + 1;
int smaller;
if (leftChildIdx > heapSize) {
return;
}
smaller = leftChildIdx;
if (rightChildIdx <= heapSize) {
if (heap[rightChildIdx].w < heap[leftChildIdx].w) {
smaller = rightChildIdx;
}
}
if (heap[idx].w <= heap[smaller].w) {
return;
}
swapElem(heap + idx, heap + smaller); // 부모 노드와 더 작은 자식 노드 교환
downHeap(heap, smaller, heapSize); // 자식 노드로 내려감
}
// 힙에서 최소 가중치 간선 추출 함수
int extractMin(HEAP* heap, int heapSize) {
if (heapSize == 0) {
return -1;
}
HEAP idxToRemove = heap[1]; // 루트 노드 추출
swapElem(heap + 1, heap + heapSize); // 루트 노드와 마지막 노드 교환
downHeap(heap, 1, heapSize - 1);
return idxToRemove.edgeIdx;
}
// 정점이 속한 집합 찾기 함수
int findSet(DISJOINTSET* set, int v) {
INCIDENT* ptr;
for (int i = 0; i < graph.n; i++) {
ptr = set[i].head; // 집합의 헤드 설정
while (ptr != NULL) { // 정점이 속한 집합 찾기
if (graph.vertex[ptr->edgeIdx].num == v) {
return i;
}
ptr = ptr->next;
}
}
return -1;
}
// 두 집합을 합치는 함수
void unionSet(DISJOINTSET* set, int u, int v) {
// 집합 크기를 비교하여 작은 집합을 큰 집합에 합침
int temp, i;
if (set[u].setSize < set[v].setSize) {
temp = u;
u = v;
v = temp;
}
// 작은 집합의 모든 정점을 큰 집합에 추가
while (1) {
i = removeIncidentNode(&(set[v].head));
if (i == -1) {
break;
}
// 정점을 큰 집합에 추가
addIncidentNode(&(set[u].head), i);
}
set[v].head = NULL; // 작은 집합의 헤드 초기화
set[v].setSize = 0; // 작은 집합의 크기 초기화
}
void swapElem(HEAP* x, HEAP* y) {
HEAP temp;
temp = *x;
*x = *y;
*y = temp;
}
void freeSet(DISJOINTSET* set) {
INCIDENT* cur;
for (int i = 0; i < graph.n; i++) {
cur = set[i].head; // 각 집합의 헤드 설정
while (cur != NULL) {
INCIDENT* temp = cur;
free(temp);
cur = cur->next;
}
}
free(set);
}
/*
6 9
1 2 3
1 3 20
2 4 25
2 5 17
3 4 34
3 5 1
3 6 12
4 5 5
5 6 37
5 7
1 2 75
1 4 95
1 3 51
2 4 9
4 3 19
4 5 42
3 5 31
*/
출처 및 참고: 알고리즘-원리와 응용(국형준교수님)
'Computer Science > 알고리즘' 카테고리의 다른 글
| [알고리즘] ep7+) 다익스트라와 벨만-포드 알고리즘 구현 (3) | 2024.07.27 |
|---|---|
| [알고리즘] ep7) 최단경로 (0) | 2024.07.26 |
| [알고리즘] ep6) 최소신장트리(MST) (0) | 2024.07.25 |
| 휴리스틱(heuristic) 알고리즘 (0) | 2024.07.25 |
| [알고리즘] ep5-3++) 분할통치법 vs DP (2) | 2024.07.24 |



