ㅁ가중그래프(weighted graph): 각 간선이 무게(weight)라 부르는 수치값을 가지는 그래프
무게의 예: 거리, 비용, 시간 등

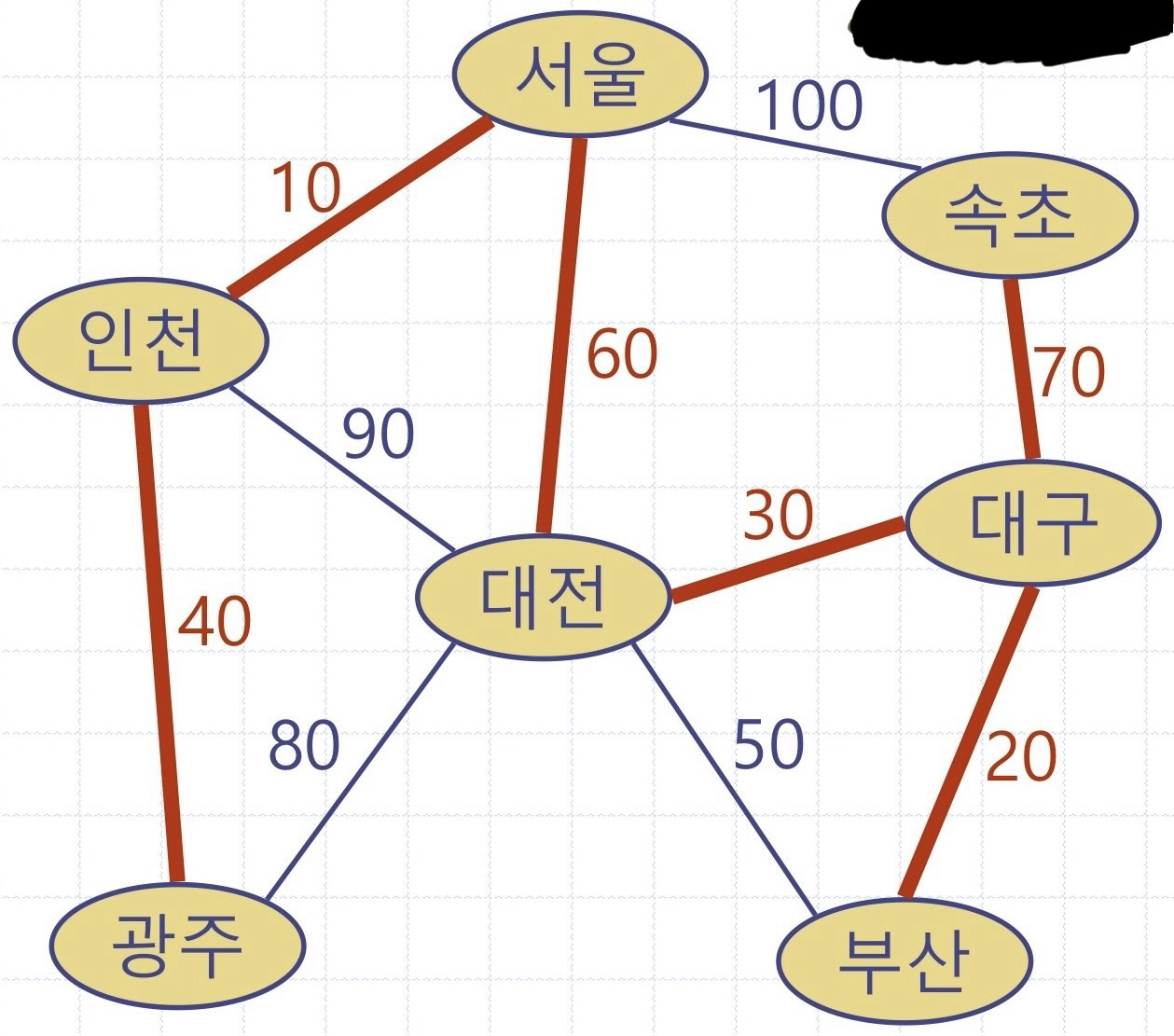
이 철도 그래프에서는 간선의 무게가 여행거리를 표현한다
신장 부그래프: 그래프 G의 모든 정점들을 포함하는 부그래프
신장트리(spanning tree): 모든 정점이 다 이어져 있으면서, 싸이클이 없는 무방향 그래프 (자유 트리인 신장 부그래프)
ㅇ최소신장트리(MST, Minimum Spanning Tree): 가중그래프의 총 간선 무게가 최소인 신장트리
응용: 통신망, 교통망
[MST 속성 2가지] - MST 알고리즘 정확성 검증에 이용
1. 싸이클 속성
T를 가중그래프 G의 MST라 하자
e를 T에 존재하지 않는 G의 간선으로, C를 T에 추가하여 형성된 싸이클로 가정
그러면 C의 모든 간선 f에 대해, weight(f) <= weight(e)

증명: 모순법
만약 weight(f) > weight(e)라면, f를 e로 대체함으로써 무게가 더 작은 신장트리를 얻을 수 있기 때문이다
2. 분할 속성
G의 정점들을 두 개의 부분집합 U와 V로 분할한다고 하자
e를 분할을 가로지르는 최소 무게의 간선이라고 하자
간선 e를 포함하는 G의 MST가 반드시 존재

증명:
T를 G의 MST라 하자
만약 T가 e를 포함하지 않는다면, e를 T에 추가하여 형성된 싸이클 C를 구성하는 간선들 가운데 분할을 가로지르는 간선 f가 존재한다
싸이클 속성에 의해 weight(f) <= weight(e) 그러므로, weight(f) = weight(e)
f를 e로 대체하면 또 하나의 MST를 얻을 수 있다
휴리스틱(heuristic) 알고리즘
ㅇ휴리스틱(heuristic): 문제 해결, 학습, 또는 발견을 위한 경험적 기법 또는 방법론 최적의 해결책을 보장하지는 않지만, 실용적으로 충분히 좋은 해결책을 빠르게 찾는 데 유용하다 [활용 분
claremont.tistory.com
ㅇ탐욕법(greedy method): 각 단계마다 가장 최적이라고 생각되는 선택을 함으로써 최종 해답에 도달하는 알고리즘
이 알고리즘의 핵심은 각 단계에서 지역적으로의 최적의 선택이 전역적으로도 최적의 해결책이 된다고 가정하는 것이다
(현재의 선택이 미래의 선택에 영향을 주지 않는 상황)
구성(configuration): 다양한 선택, 모음 또는 찾아야 할 값들
목표(objective): 구성에 할당된 점수가 존재하며, 이를 최대화 또는 최소화해야 하는 상황
탐욕적 선택 속성(greedy-choice property)을 가진 문제에 적용할 경우 가장 잘 맞는다
- 출발 구성으로부터 시작하여 지속적인 지역적 향상을 통해 전체 최적해를 항상 찾을 수 있다
e.g. 잔돈 거스르기, 부분적 배낭 문제, MST 문제
[잔돈 거스르기 문제]
구성: 거슬러줘야 할 금액 정보, 종류별 여러 개의 동전들
목표: 동전 수를 최소화
탐욕해: 가능하면 항상 제일 큰 동전으로 거슬러준다
"만약 이 문제가 탐욕적 선택 속성을 가졌다면 탐욕해는 최적해가 된다"
예시1) 동전 종류가 32원, 8원, 1원인 경우
탐욕적 선택 속성이 있음. 왜냐하면 32원 이상의 금액은 32원을 빼고는 최소 수의 동전으로 만들 수가 없기 때문 (8원을 넘지만 32원을 못 미치는 금액에 대해서도 마찬가지)
예시2) 동전 종류가 30원, 20원, 5원, 1원인 경우
탐욕적 선택 속성이 없음. 왜냐하면 40원은 두 개의 20원만으로 만들 수 있으나, 탐욕해는 세 개의 동전을 택하기 때문
[부분적 배낭 문제(the fractional knapsack problem)] - 각 항목의 일부만을 취할 수 있는 문제
흔히 ps에서 "냅색"이라 말한다
구성: n항목의 집합 S
- bi: 양수의 이득
- vi: 양수의 부피
목표: 최대 부피 한도 V내에서, 최대의 총이득을 주는 항목들을 선택
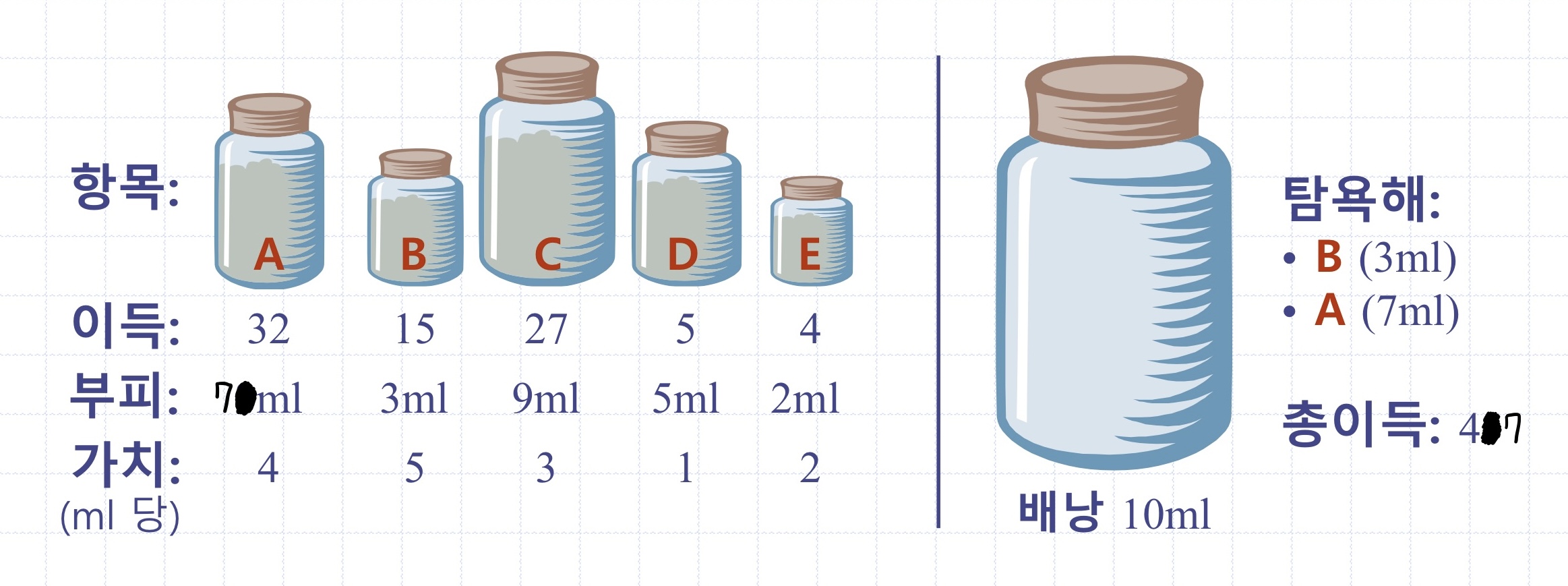
(추가)
0-1 배낭 문제(all-or-nothing knapsack problem) - 각 항목의 일부만을 취할 수 없는 문제
0-1 배낭 문제는 탐욕적 선택 속성을 만족하지 않는다 >> DP로 해결
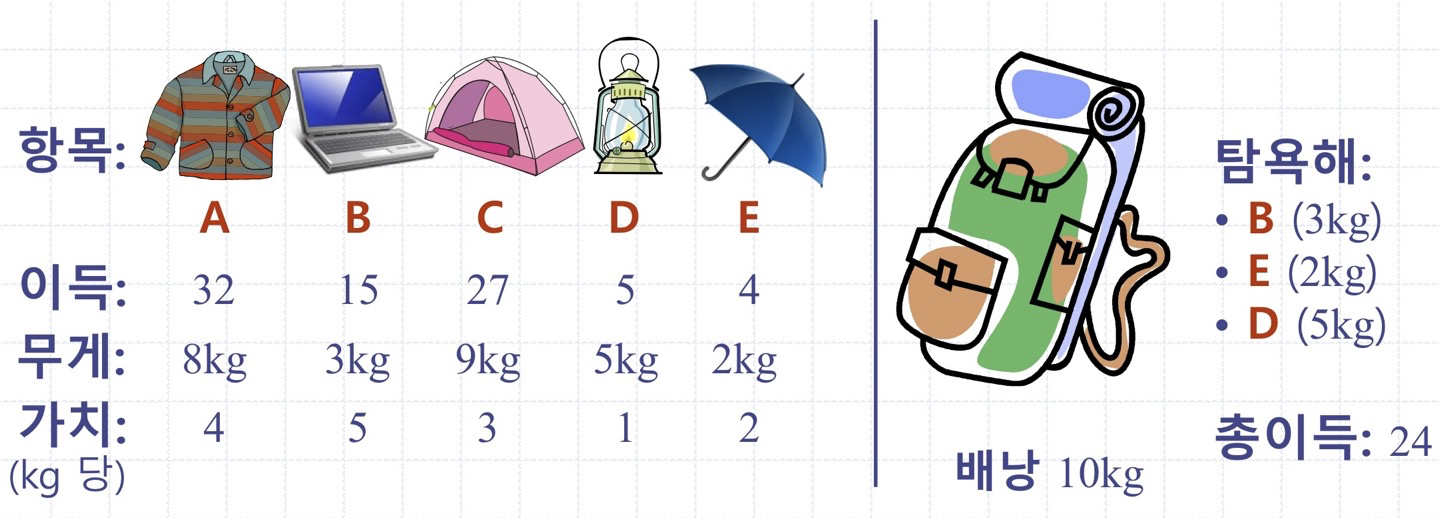
최적해는 이득 = 36 을 가져다주는 {A, E}지만, 탐욕해는 이득 = 24 를 가져다주는 {B, E, D}를 고른다
[MST 알고리즘]
① Prim-Jarnik 알고리즘 - 매 단계마다 가장 작은 가중치의 간선을 선택하여 점진적으로 MST를 확장
배낭 밖의 정점들을 우선순위 큐에 저장
대상: 단순 연결 무방향 가중그래프
임의의 정점 s를 택하여 s로부터 시작하여 정점들을 (가상의) 배낭에 넣어가며 배낭 안에서 MST T를 키워 나간다 - s는 T의 루트가 된다
각 정점 v에 라벨 d(v)를 정의 - d(v)는 배낭 안의 정점과 배낭 밖의 정점을 연결하는 간선의 무게
반복의 각 회전에서 배낭 밖의 정점들 가운데 최소 d(z) 라벨을 가진 정점 z를 배낭에 넣는다 + z에 인접한 정점들의 라벨을 갱신
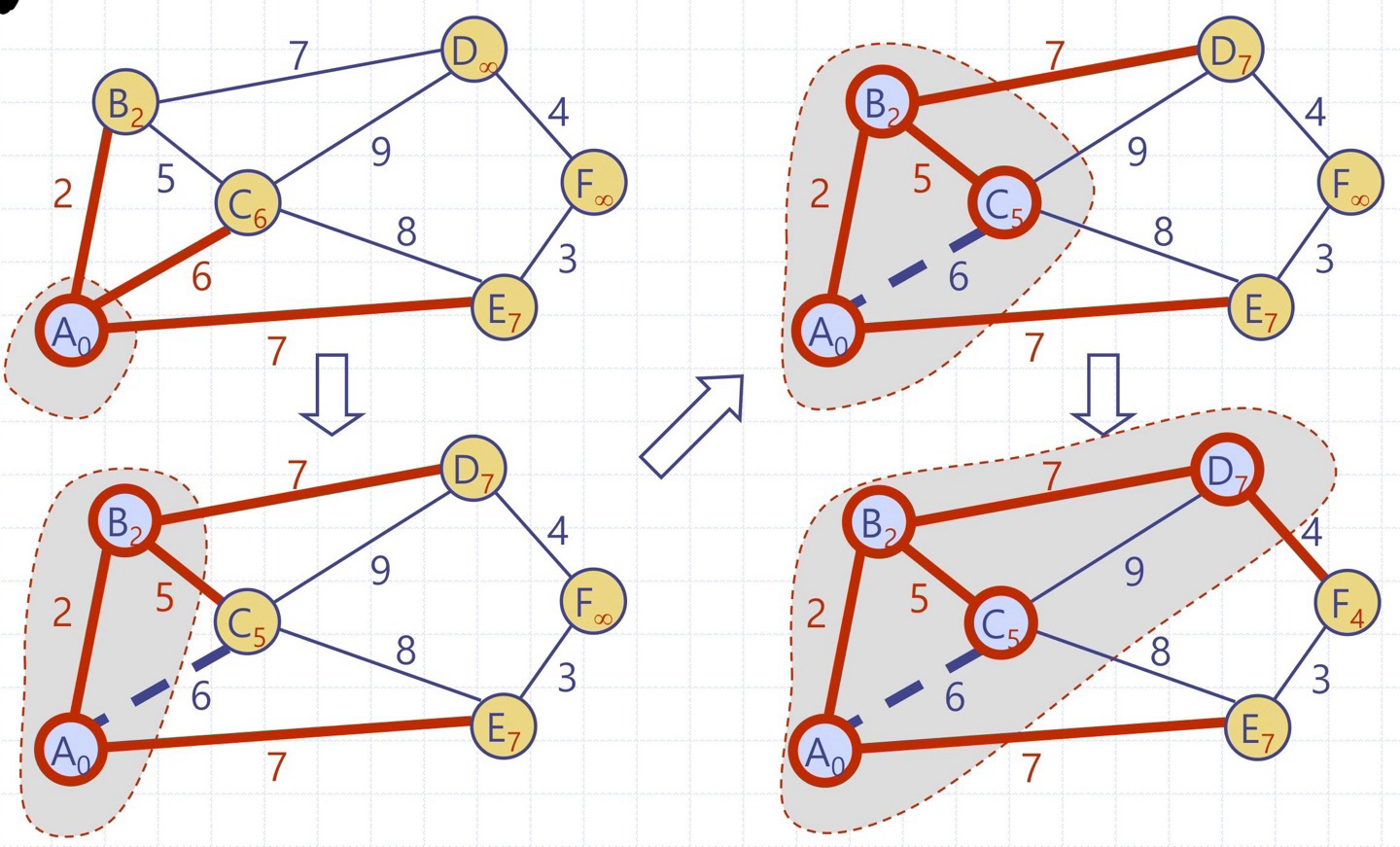
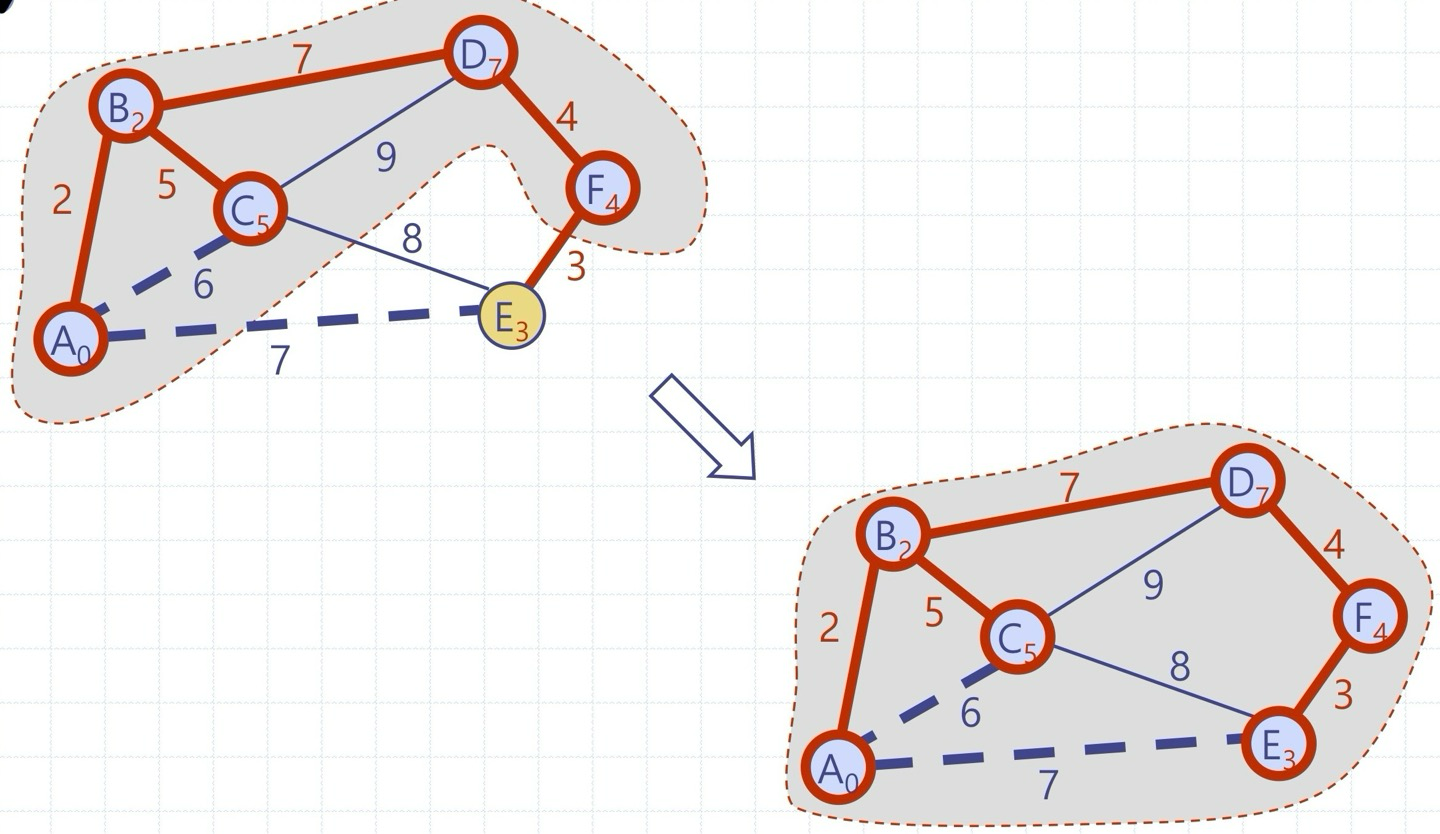
Prim-Jarnik 알고리즘은 반복의 각 회전에서 항상 배낭 C안의 정점을 배낭 C밖의 정점과 이어주는 최소 무게의 간선을 선택하므로, MST에 항상 타당한 간선을 추가한다 따라서 MST에 관한 분할 속성 요건을 만족!
② Kruskal 알고리즘 - 모든 간선을 가중치에 따라 정렬한 후, 가중치가 가장 작은 간선부터 차례로 선택하여 MST를 구성
이때, 사이클이 생기지 않도록 간선을 선택하는 것이 핵심
모든 정점을 각각의 독자적인 (실제의) 배낭에 넣는다
배낭 밖의 간선들을 우선순위 큐에 저장한다 (키: 무게, 원소: 간선)
비어 있는 MST T를 초기화한다
반복의 각 회전에서 두 개의 다른 배낭 속에 양끝점을 가진 최소 무게의 간선을 MST T에 포함하고 두 배낭을 하나로 합친다
반복이 완료되면 MST T를 포함하는 한 개의 배낭만 남는다
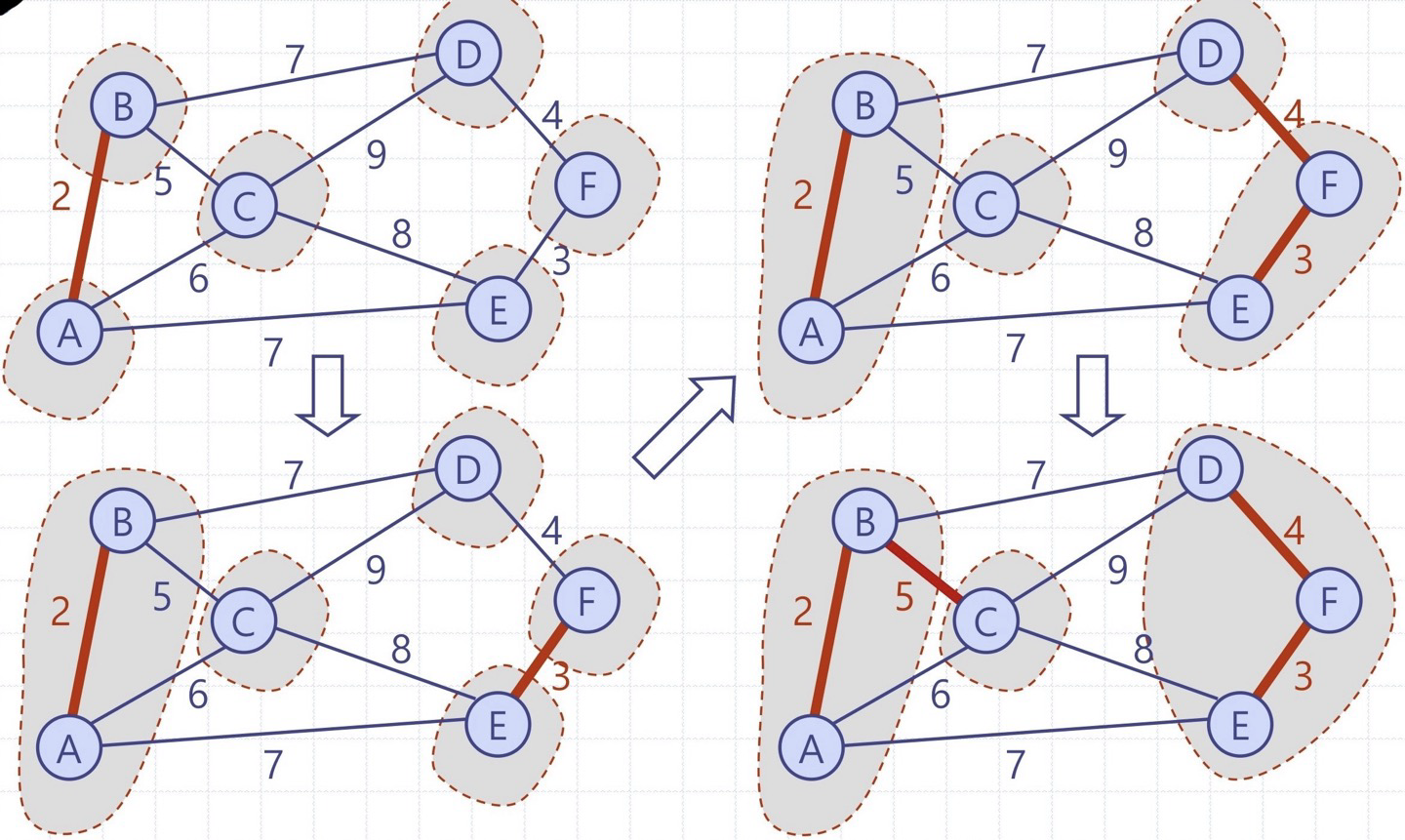
Kruskal 알고리즘의 정확성은 분할 속성으로부터 유도된다
Kruskal 알고리즘은 반복의 회전마다 간선 (u, v)를 MST T에 추가한다
이때 정점 집합 V가 u를 포함하는 배낭 V1과 V1에 속하지 않은 나머지 정점들을 모두 포함하는 배낭 V2로 분할되었다고 보면, 이는 모든 정점이 두 부분으로 분리된 분할된 분할 상태이다
Q로부터 간선들을 무게 순서로 추출하고 있으므로, (u, v)는 양 끝점이 각각 V1과 V2에 속한 최소 무게의 간선이다
따라서 Kruskal 알고리즘은 항상 타당한 MST 간선을 추가한다
(Kruskal 알고리즘을 구현하기 위한 자료구조)
1. Kruskal 알고리즘은 인접 정보를 사용하지 않는다, 따라서 인접 정보(인접리스트 or 인접행렬)가 생략된 간선리스트 구조로 표현된 그래프에서 수행 가능하다
2. Kruskal 알고리즘은 트리들의 숲을 유지한다, 각 트리들을 리스트로 구현된 분리집합에 저장하고 각 원소에 소속 집합을 가리키는 참조를 저장한다
- find 함수: 소속 집합 검사
- union 함수: 배낭 합치기 수행
https://www.youtube.com/watch?v=klBh4ZglHYo&list=PLFgS-xIWwNVX-zm4m6suWC9d7Ua9z7fuT&index=29
분리집합(유니온 파인드)에 대해 이 영상을 참고하자 정말 좋은 영상이다
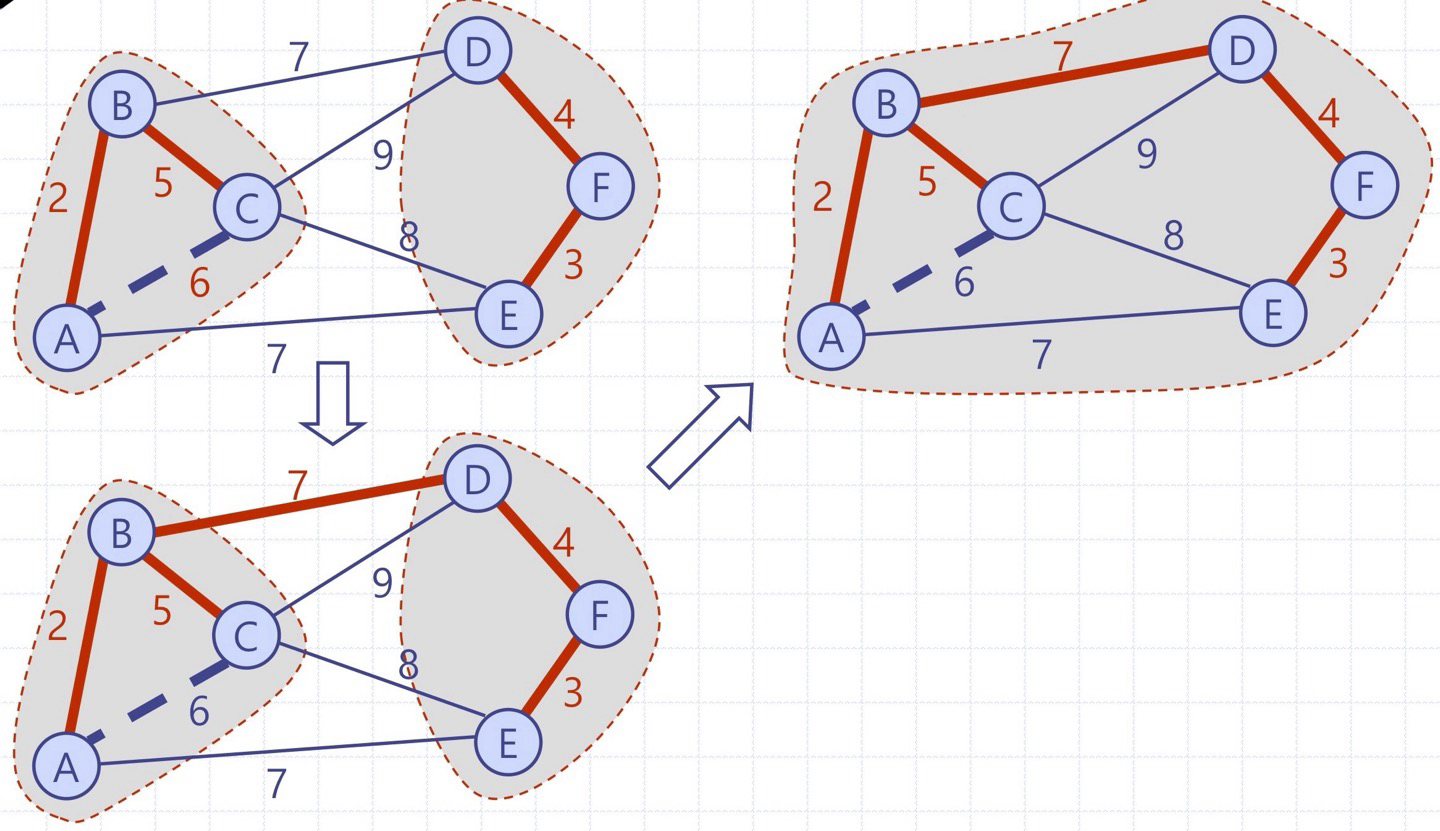
③ Baruvka 알고리즘 (a.k.a. Sollin 알고리즘) - 각 단계에서 모든 연결 요소가 가장 작은 가중치의 간선을 선택하여 점차적으로 연결 요소를 병합하는 방식
Prim-Jarnik이나 Kruskal 알고리즘과 달리 우선순위 큐 사용 X
Kruskal 알고리즘과 마찬가지로 Baruvka 알고리즘도 모든 정점을 각각의 독자적인 (실제의) 배낭에 넣고 시작
Prim-Jarnik이나 Kruskal 알고리즘이 반복의 각 회전에서 한 개의 간선을 취함으로써 배낭을 키워나가는 것과 달리, 한꺼번에 여러 개의 간선을 취하여 여러 수의 배낭을 동시에 키워 나감

Baruvka 알고리즘 반복의 각 단계에서는, 현재의 MST T의 각 연결요소 Ci 사이를 교차하는 최소 무게의 간선들을 취한다
여기서 V가 Ci에 속한 정점들과, Ci 바깥의 정점들로 분할되었다고 가정하면, Ci를 위해 선택된 간선 e는 e가 MST에 반드시 포함되어야 한다는 MST에 관한 분할 속성의 요건을 만족한다
따라서 반복의 각 단계에서 취해지는 간선들은 모두 타당한 선택이 된다
출처 및 참고: 알고리즘-원리와 응용(국형준교수님), Algorithm Design(Jon Kleinberg, Eva Tardos), Foundations of Algorithms using C++(Richard Neapolitan)
'Computer Science > 알고리즘' 카테고리의 다른 글
| [알고리즘] ep7) 최단경로 (0) | 2024.07.26 |
|---|---|
| [알고리즘] ep6+) Prim-Jarnik과 Kruskal 알고리즘 구현 (0) | 2024.07.26 |
| 휴리스틱(heuristic) 알고리즘 (0) | 2024.07.25 |
| [알고리즘] ep5-3++) 분할통치법 vs DP (2) | 2024.07.24 |
| [알고리즘] ep5-3+) 위상순서 찾기 (7) | 2024.07.24 |



