복습하고 오자!
https://claremont.tistory.com/entry/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-ep1-3-%ED%9E%99heap
[알고리즘] ep1-3) 힙(heap)
*완전 이진 트리(Complete Binary Tree): 트리의 위부터 아래, 왼쪽부터 오른쪽의 순서로 빠짐없이 가득 차있는 이진 트리 ㅁ힙(heap): 가장 크거나 가장 작은 값을 빠르게 찾기 위해 만든 완전 이진 트
claremont.tistory.com
ㅇ힙정렬(heap sort): 힙을 이용하여 정렬하는 방식
"제자리 + unstable" O(nlog(n))
1. 원소들을 전부 힙에 삽입한다.
2. 힙의 루트는 남은 수들 중에서 최솟값(or 최댓값)을 가지므로 루트를 출력하고 힙에서 제거한다.
3. 힙이 빌 때까지 2의 과정을 반복한다.
[heap sort의 성능 향상을 위한 두 가지 개선점]
- 제자리(in-place) 힙정렬은 heap sort의 공간 사용을 줄인다
- 상향식 힙생성은 heap sort의 속도를 높인다
무순리스트(unordered list)에 대한 힙 정렬은 두 단계로 진행된다
1기: 힙 생성 단계로서 초기 리스트로부터 최대힙을 생성
2기: 힙 정렬 단계로서 전 단계에서 생성된 최대힙으로부터 오름차순 정렬을 수행
1기에서 생성되는 힙은 삽입식 또는 상향식 가운데 한 방식을 사용하여 각각 순차힙 또는 연결힙 둘 중 한 형태로 생성할 수 있다.
만약 순차힙으로 구현한다면, 1기와 마찬가지로 2기에서도 제자리 힙 정렬이 가능하다. 즉, 추가 메모리를 사용하지 않고 초기 배열 내에서 정렬을 완성할 수 있다.
반대로 연결힙으로 구현한다면, 1기에서 초기 리스트의 키들에 대해 동적메모리 노드들을 할당하여 힙을 생성한다. 그리고 2기를 진행하는 동안 힙 정렬의 결과를 초기 리스트에 다시 저장하여 반환해야 한다.
[1기]: 힙 생성 단계 - 초기 리스트로부터 최대힙을 생성
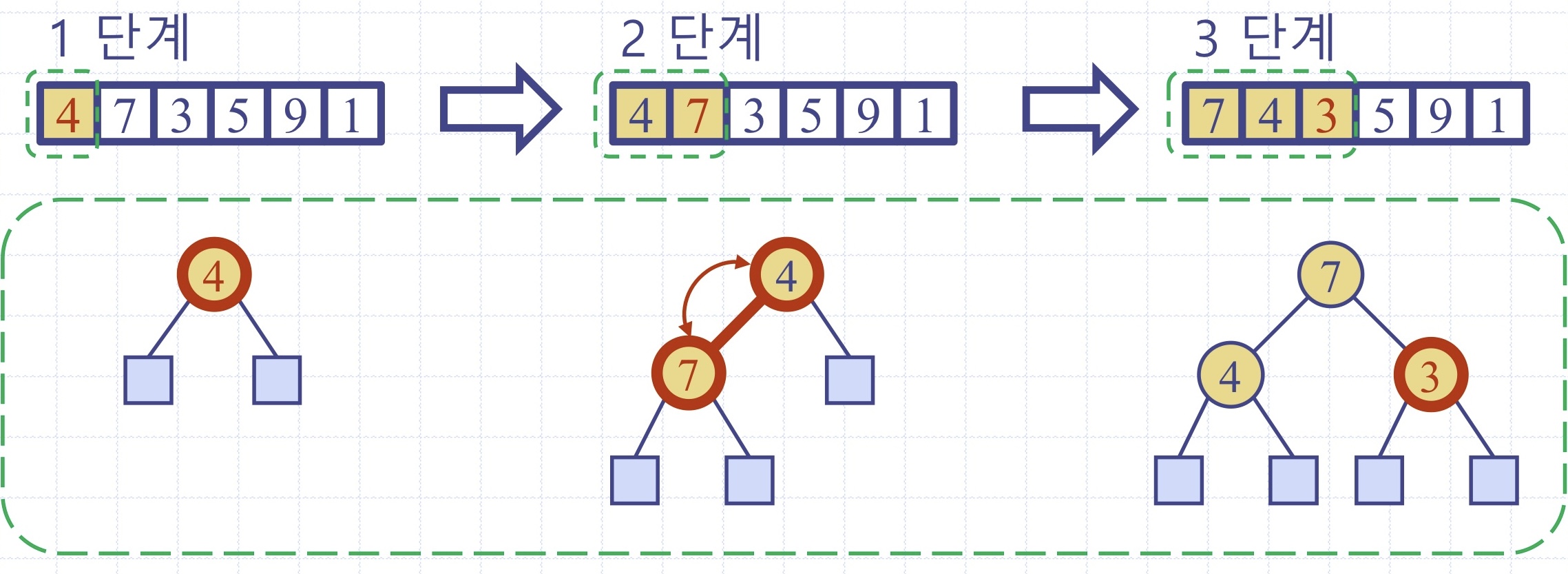


[2기]: 힙 정렬 단계 - 최대힙으로부터 오름차순 정렬을 수행




ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ
문제) 삽입식 힙 생성 후 정렬 - 유일 키, 중복 키 모두 ok
1) 순차힙으로 구현한다. 즉, 배열을 이용한 순차트리 형식으로 힙을 저장한다.
2) 연산 효율을 위해 배열 인덱스 0 위치는 사용하지 않고 비워둔다.
3) 데이터구조를 단순화하기 위해 힙의 항목으로써 (키, 원소) 쌍에서 원소를 생략하고 키만 저장하는 것으로 한다.
4) 최대 키 개수 < 100 으로 전제한다.
5) 1기(힙 생성 단계)에서 삽입식으로 힙을 생성한다.
6) O(n log n) 시간, O(1) 공간에 수행해야 한다.
7) 키들은 중복이 있을 수 있는 1 이상의 정수로 전제한다.

(전체코드)
// 삽입식 힙 생성 후 정렬 - 유일 키, 중복 키 모두 ok
#include <stdio.h>
#define MAX_HEAP_SIZE 99
int g_heap[MAX_HEAP_SIZE]; // 배열구조의 힙
int g_n = 0; // 힙의 크기(현재 총 키의 개수)
void insertItem(int key);
void upHeap(int idx);
void downHeap(int idx);
void inPlaceHeapSort();
void printArray();
int main() {
int numKeys, key;
scanf("%d", &numKeys);
for (int i = 1; i <= numKeys; i++) {
scanf("%d", &key);
insertItem(key);
}
inPlaceHeapSort();
printArray();
return 0;
}
void insertItem(int key) {
g_n++;
g_heap[g_n] = key;
upHeap(g_n);
}
void upHeap(int idx) {
int parentIdx;
int temp;
while (idx > 1 && g_heap[idx] > g_heap[idx / 2]) { // g_heap[idx] > g_heap[parentIdx]
parentIdx = idx / 2;
temp = g_heap[idx];
g_heap[idx] = g_heap[parentIdx];
g_heap[parentIdx] = temp;
idx = parentIdx;
}
}
// 인덱스 1부터 시작하여 힙을 재구성
void downHeap(int idx) {
int temp;
int largerChildIdx; // leftChildIdx or rightChildIdx
int leftChildIdx, rightChildIdx;
while (2 * idx <= g_n) { // leftChildIdx <= g_n
leftChildIdx = 2 * idx;
rightChildIdx = 2 * idx + 1;
if (rightChildIdx <= g_n && g_heap[rightChildIdx] > g_heap[leftChildIdx])
largerChildIdx = rightChildIdx;
else
largerChildIdx = leftChildIdx;
if (g_heap[idx] >= g_heap[largerChildIdx])
break;
temp = g_heap[idx];
g_heap[idx] = g_heap[largerChildIdx];
g_heap[largerChildIdx] = temp;
idx = largerChildIdx;
}
}
void inPlaceHeapSort() {
int temp;
int tempN = g_n;
for (int i = g_n; i > 1; i--) {
// 루트(최대값)와 끝 값을 교환
temp = g_heap[1];
g_heap[1] = g_heap[i];
g_heap[i] = temp;
g_n--;
// downHeap으로 다시 힙을 구성
downHeap(1);
}
g_n = tempN; // 정렬 후 원래 크기로 복원
}
void printArray() {
for (int i = 1; i <= g_n; i++) {
printf(" %d", g_heap[i]);
}
printf("\n");
}
/*
3
209 400 77
6
24 17 33 50 60 70
8
5 15 10 20 30 25 31 29
*/
출처 및 참고: 알고리즘-원리와 응용(국형준교수님), Algorithm Design(Jon Kleinberg, Eva Tardos), Foundations of Algorithms using C++(Richard Neapolitan)
'Computer Science > 알고리즘' 카테고리의 다른 글
| [알고리즘] ep1-6) 퀵정렬(quick sort) (0) | 2024.07.07 |
|---|---|
| [알고리즘] ep1-5) 병합정렬(merge sort) (1) | 2024.07.05 |
| [알고리즘] ep1-3) 힙(heap) (0) | 2024.07.03 |
| [알고리즘] ep1-1) 우선순위 큐 (0) | 2024.07.03 |
| [알고리즘] ep1-2) 버블정렬, 선택정렬, 삽입정렬 (1) | 2024.07.02 |



