ㅇ퀵정렬(quick sort): 분할통치법에 기초한 정렬 알고리즘
"제자리 + unstable" O(nlog(n))
※ 최악의 시간 복잡도: O(n^2) (이미 정렬된 리스트에서 항상 최악의 피벗을 선택하는 경우)
이름에서 알 수 있듯이 복잡하지만 매우 효율적인 알고리즘이다 일각에서는 이렇게 지칭한다 '살아있는 레전드'
*피벗(pivot): 기준점
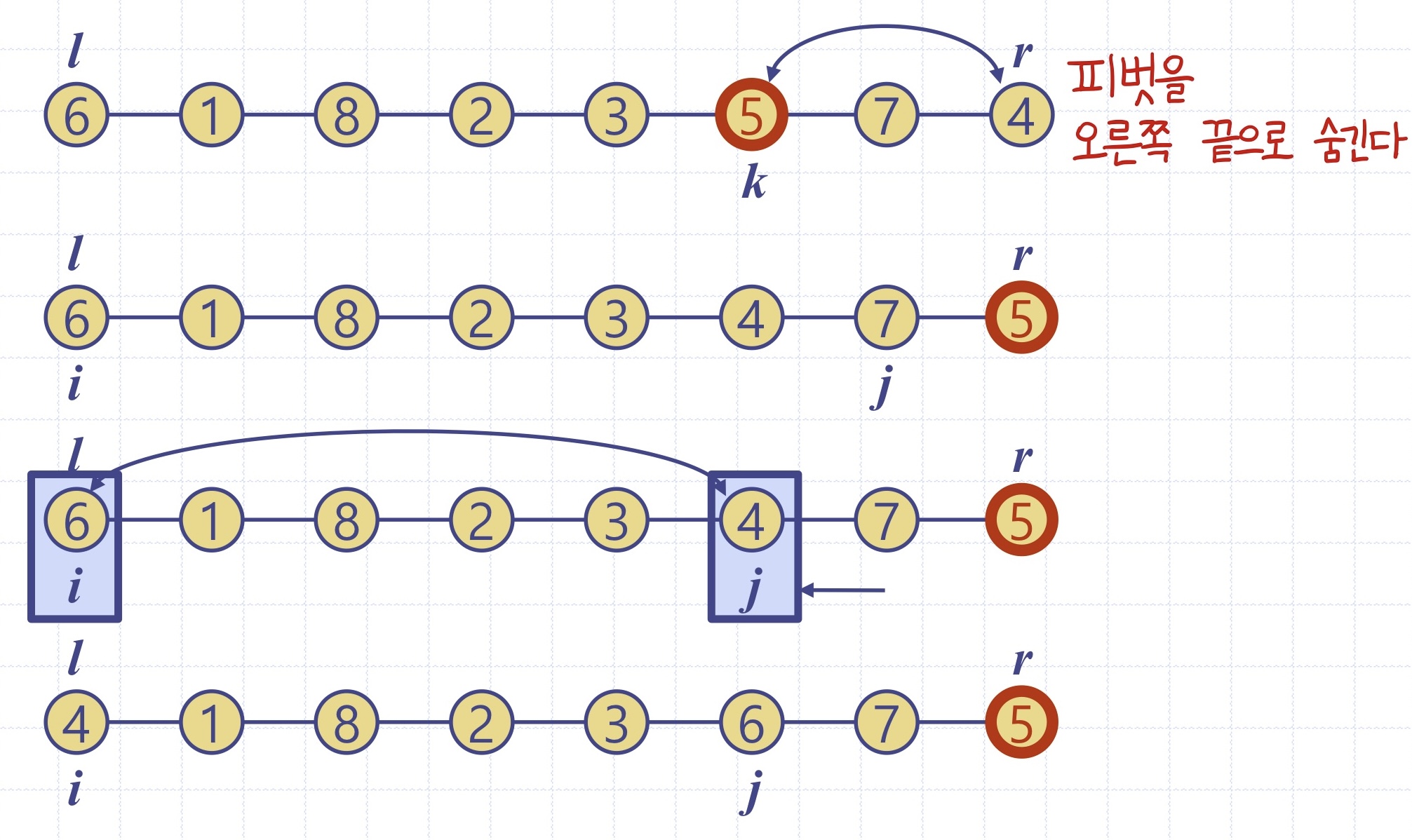
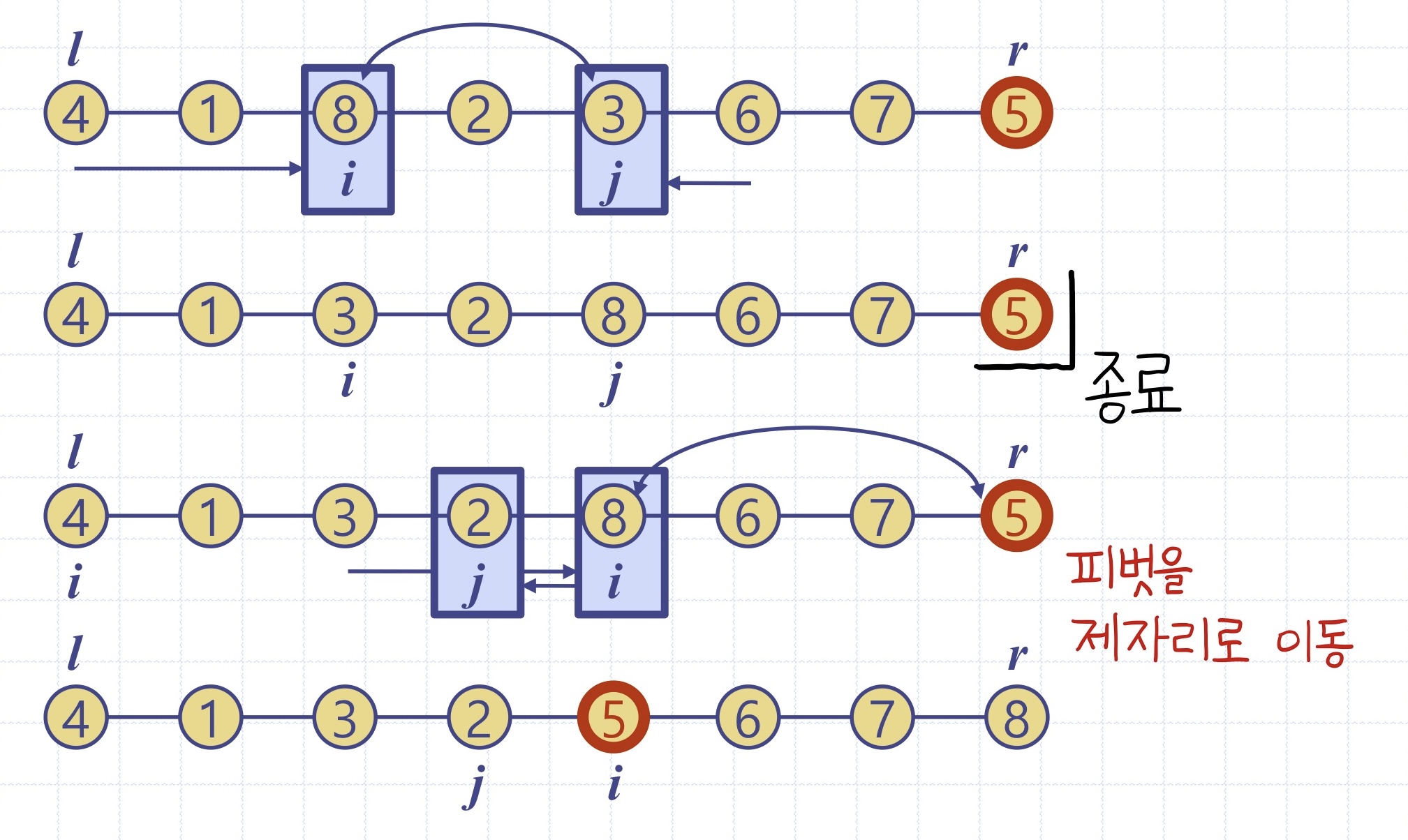
1. 피벗을 기준점으로 잡는다
2. 피벗보다 작으면 왼쪽에, 피벗보다 크면 오른쪽에 둔다
3. 왼쪽과 오른쪽을 각각 정복한다
[분할 함수(partition 함수) 과정]
다양한 피봇 선정 방식 -> 다양한 퀵소트 버전
(참고)
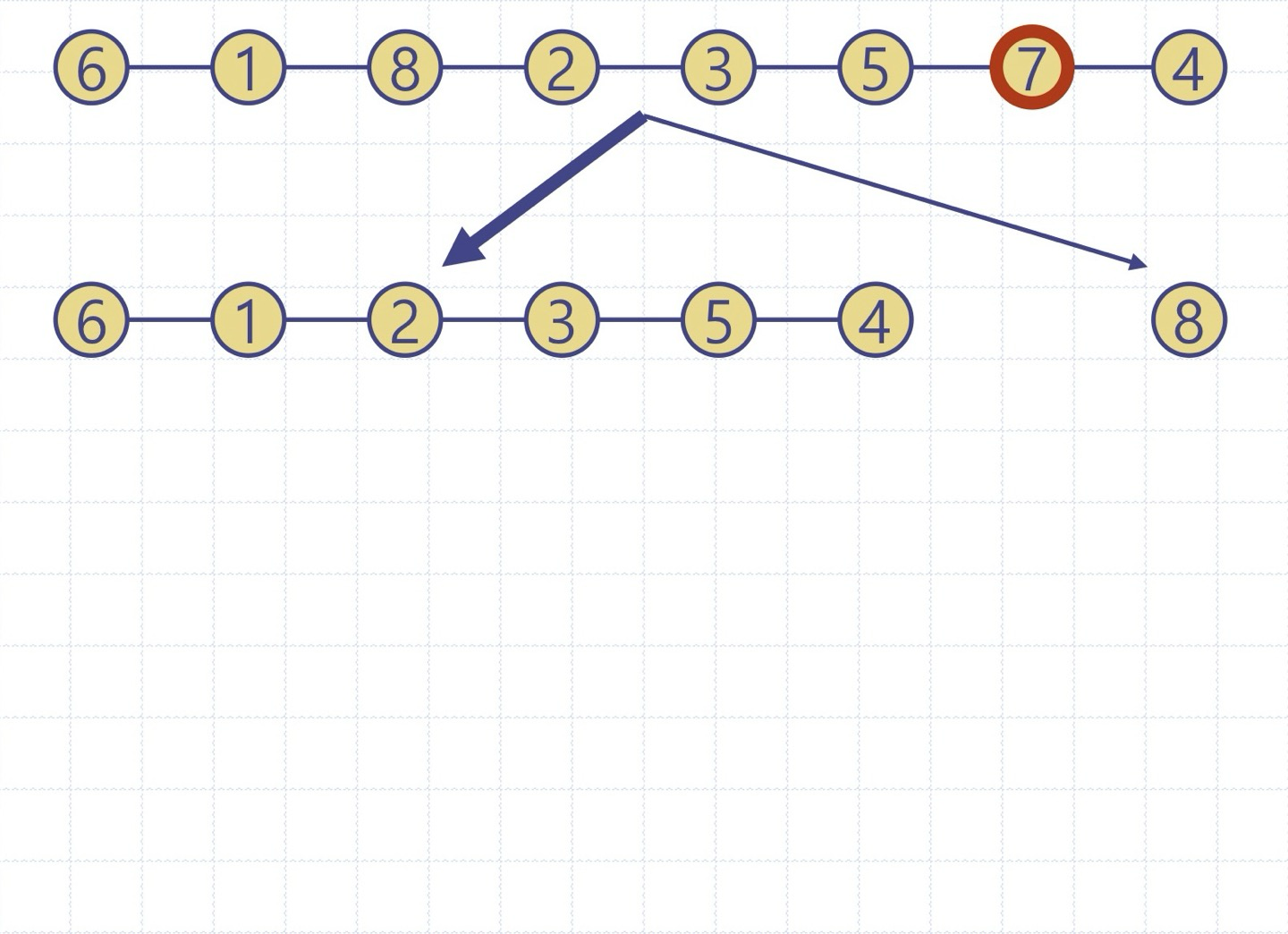
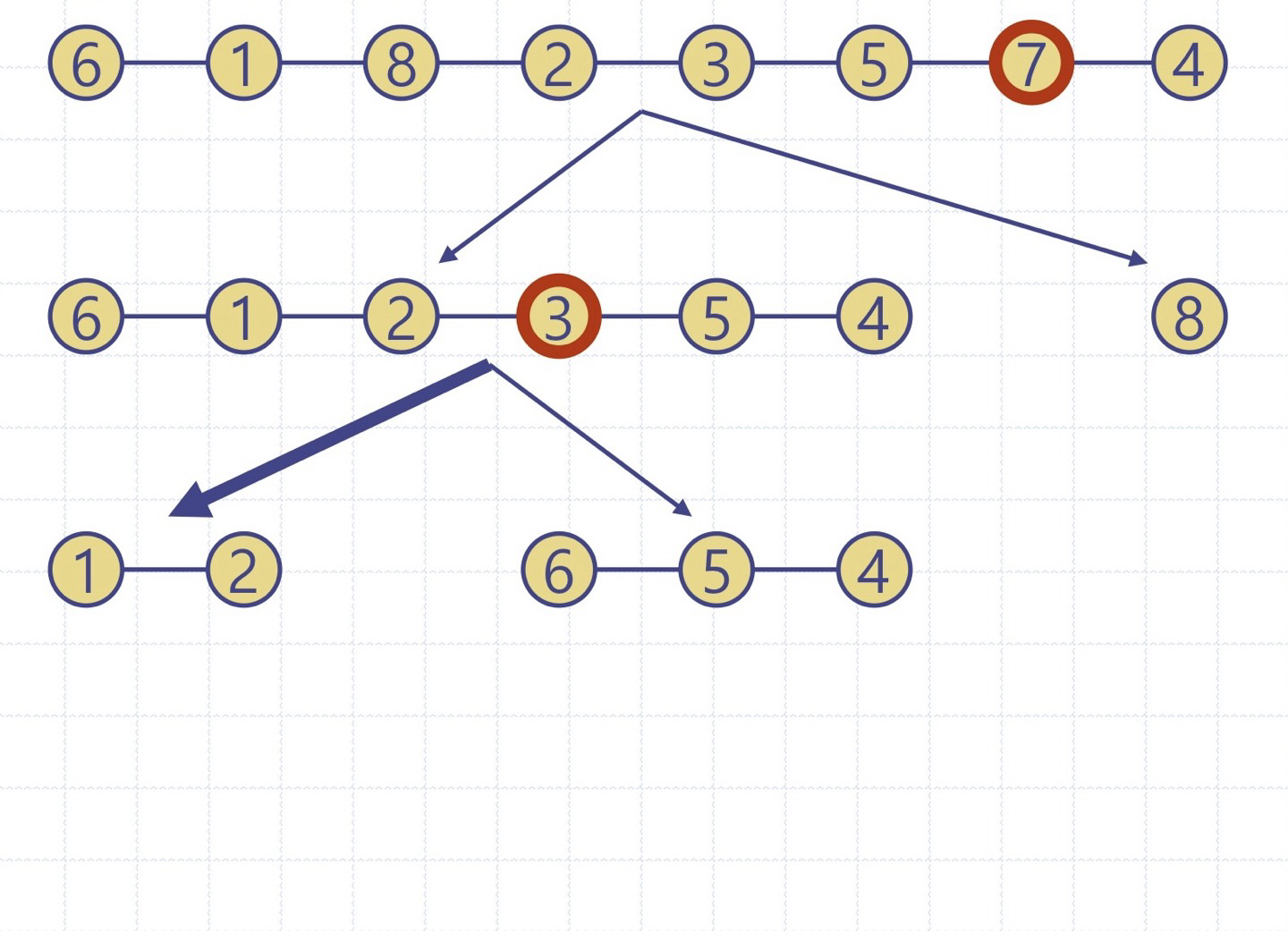
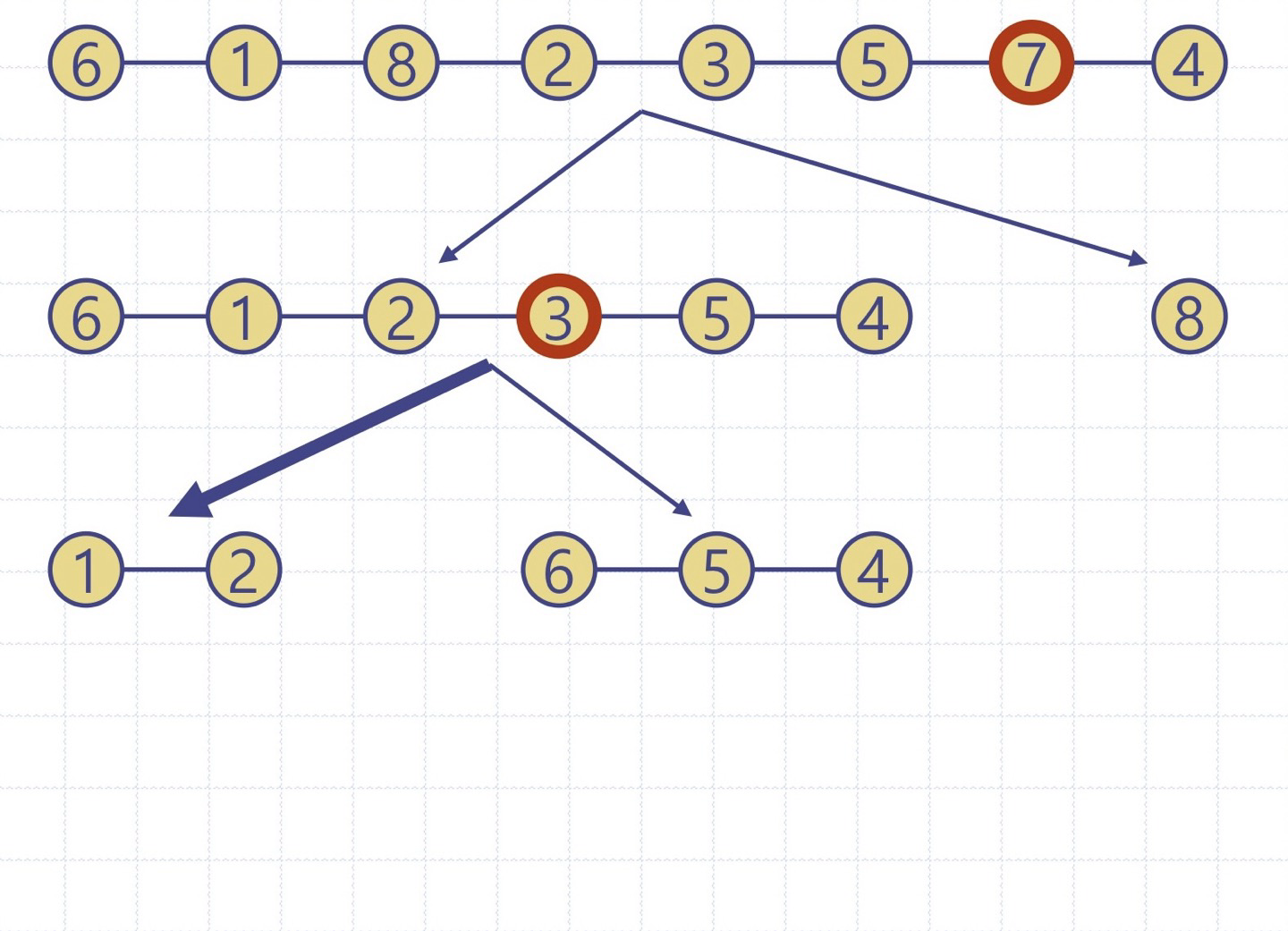
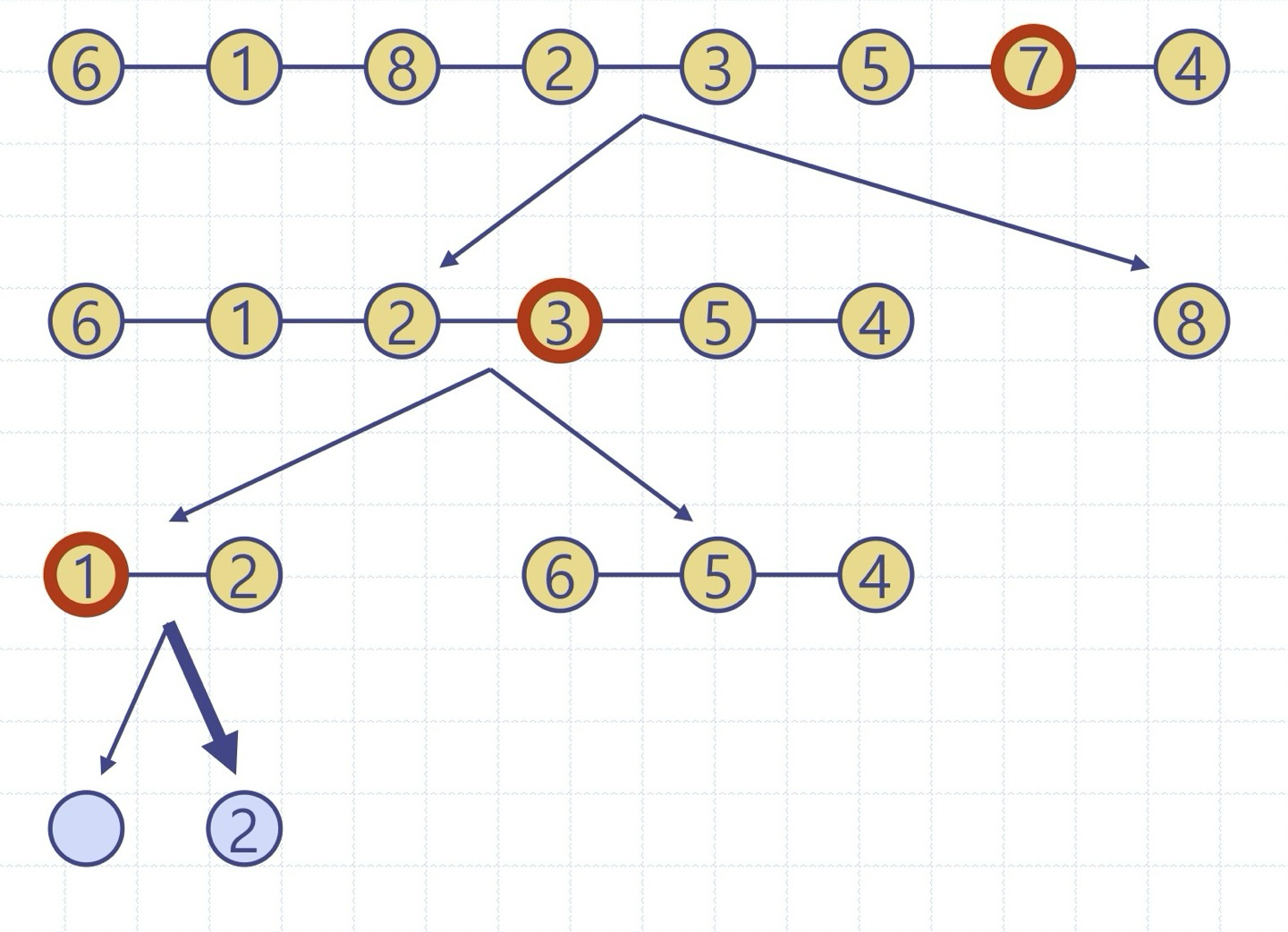
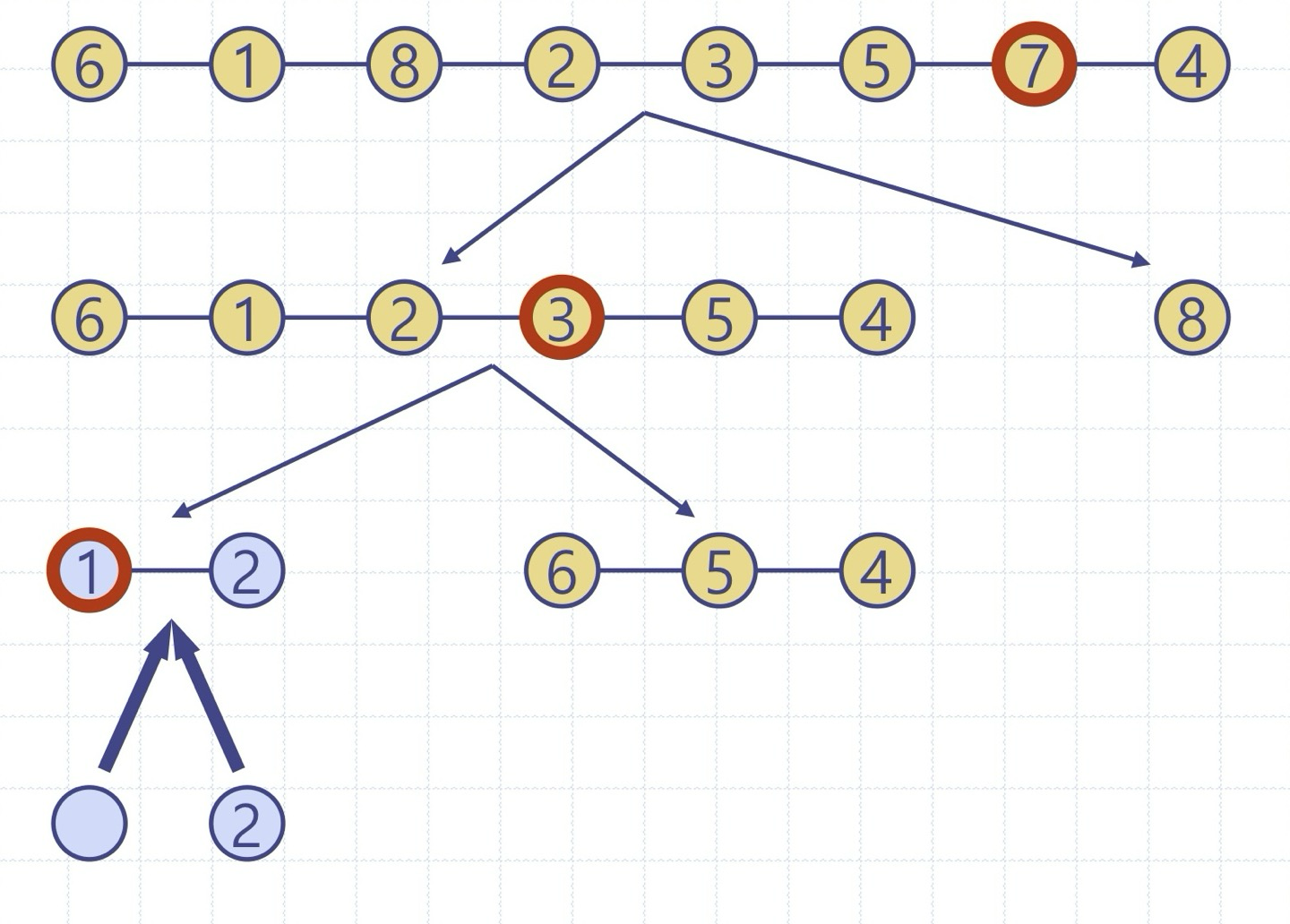
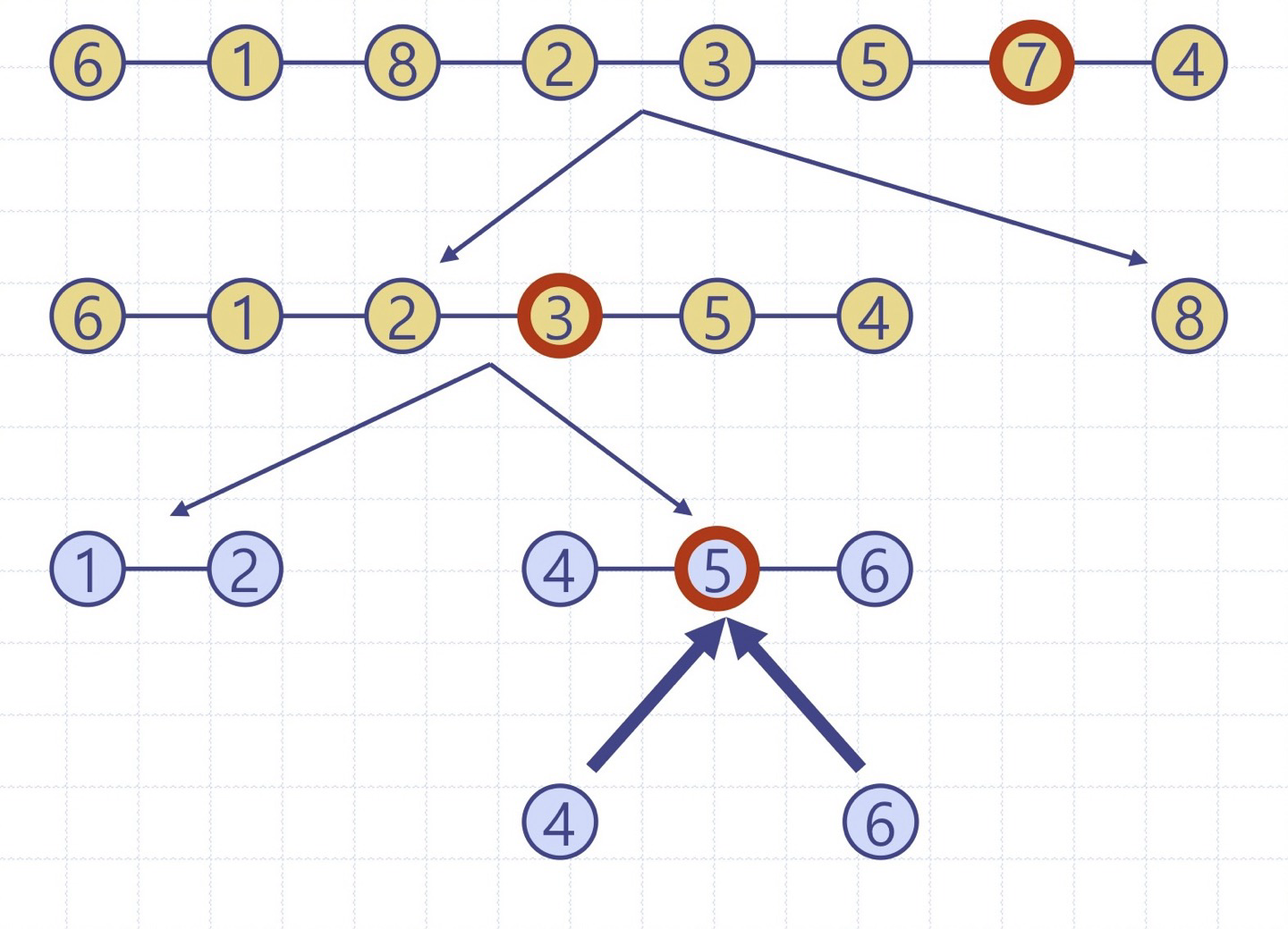
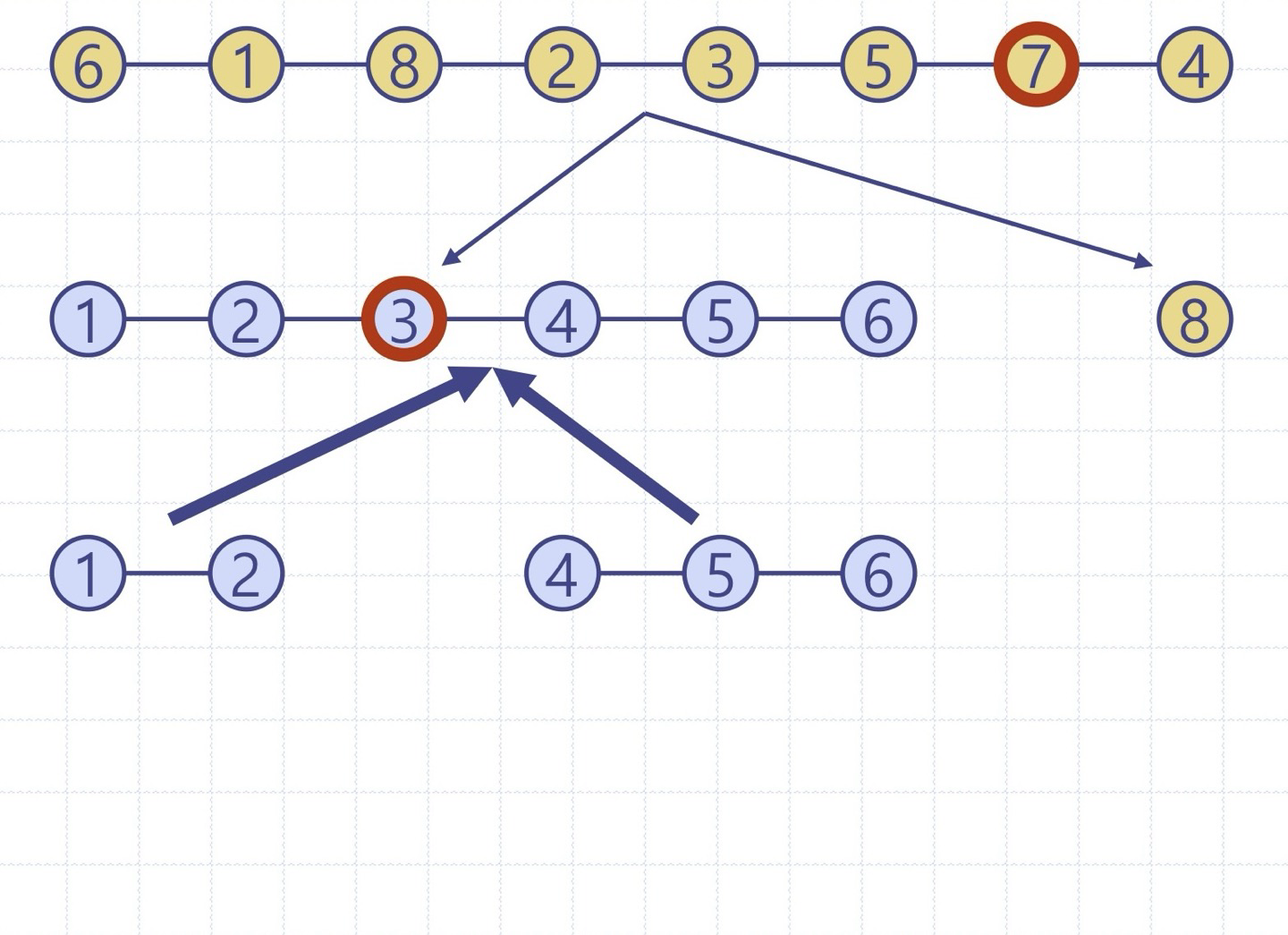
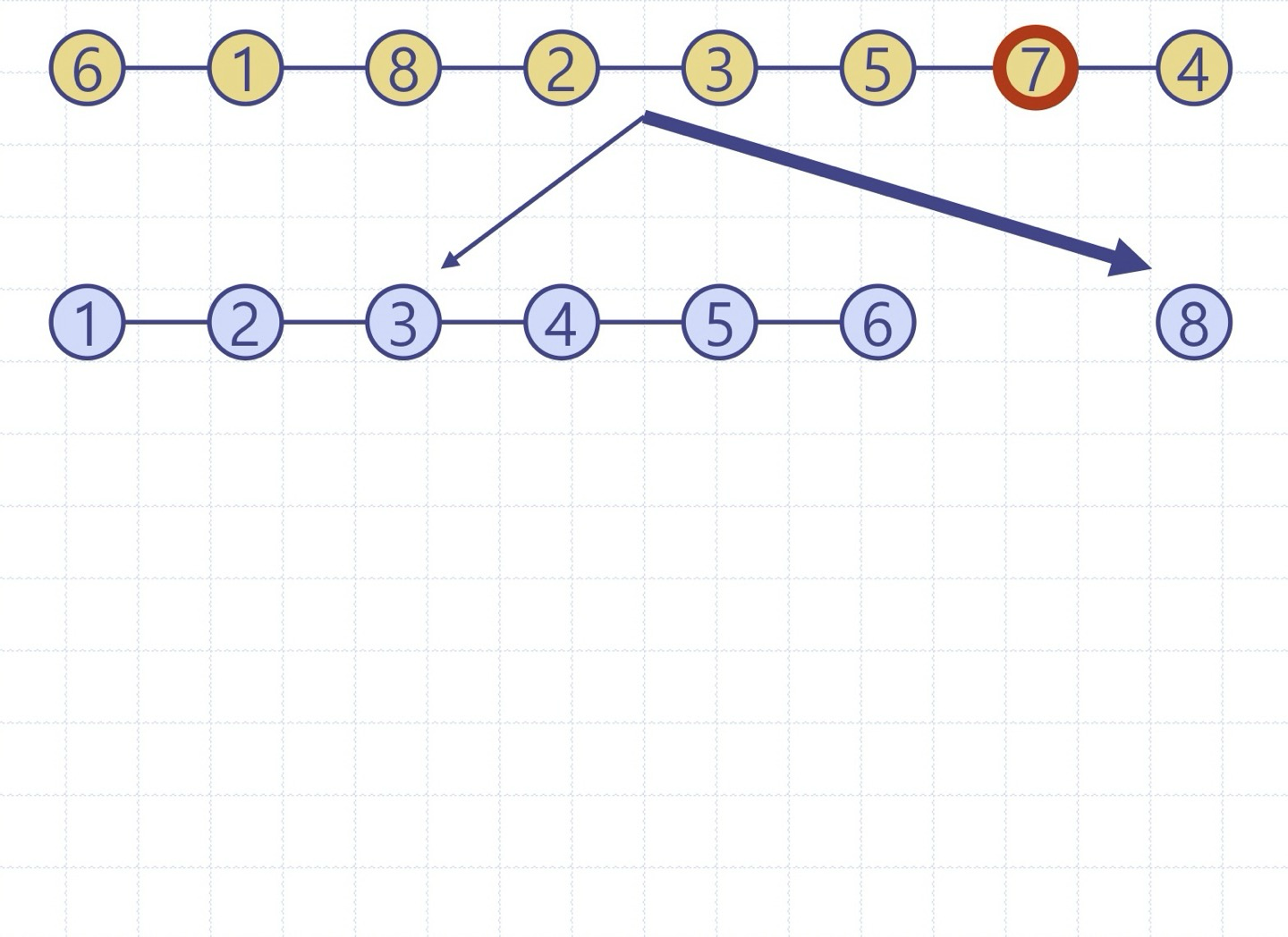
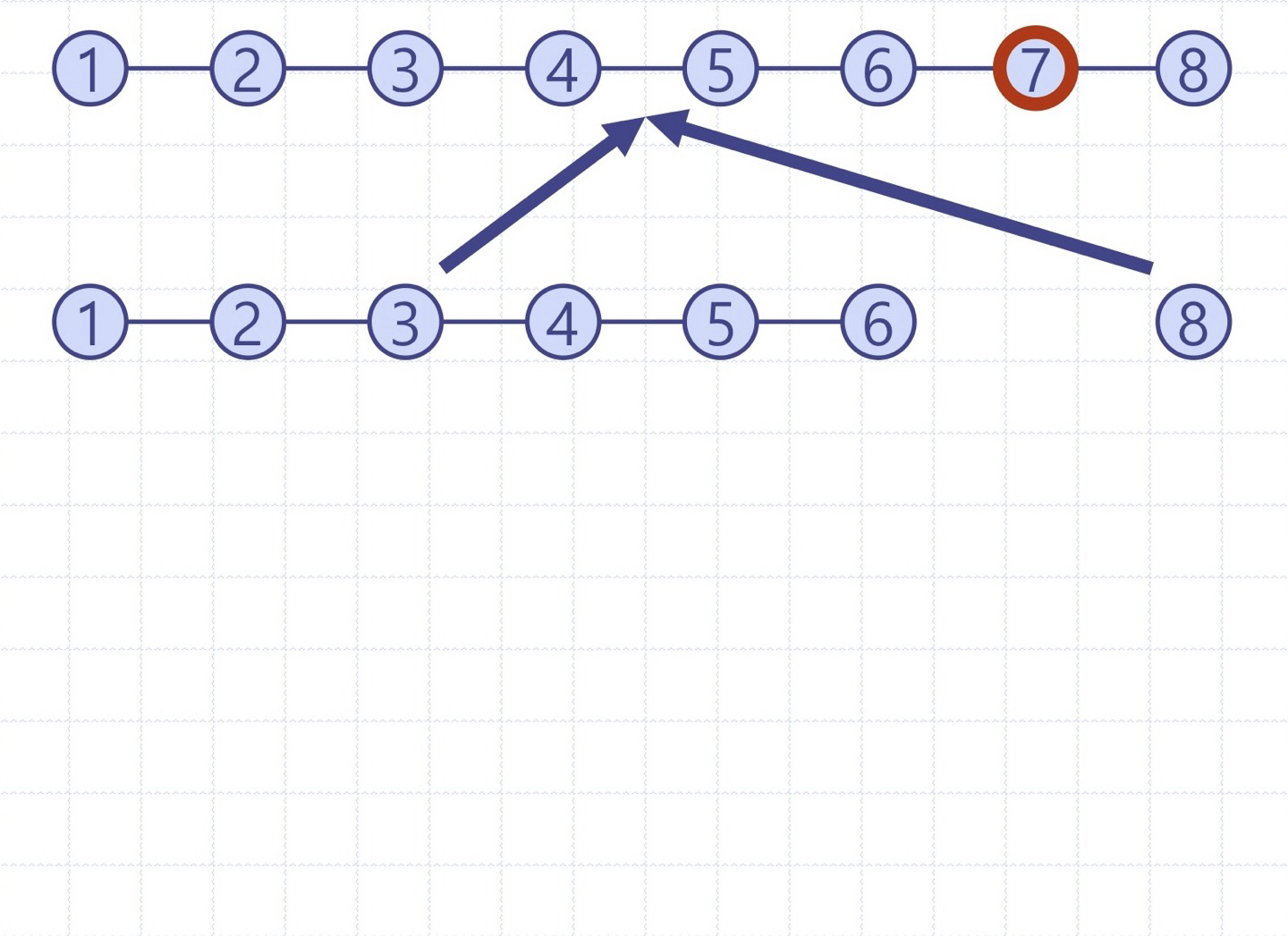
퀵정렬 트리: quickSort의 실행을 이진트리로 보이기
이진트리의 각 노드는 quickSort의 재귀호출을 표현하며 다음을 저장
- 실행 이전의 무순 리스트 및 기준원소
- 실행 이후의 정렬 리스트
루트는 초기 호출을 의미
리프들은 크기 0 or 1의 부리스트에 대한 호출을 의미
(퀵정렬 구현 코드)


#include <stdio.h>
#include <stdlib.h>
#include <time.h>
int* arr;
int chooseRandomPivotIdx(int l_idx, int r_idx);
void inPlaceQuickSort(int l_idx, int r_idx);
void inPlacePartition(int l_idx, int r_idx, int pivotIdx, int* l_PartitionEndIdx, int* r_PartitionStartIdx);
void swap(int* ptr1, int* ptr2);
void printArray(int n);
int main() {
int n;
scanf("%d", &n);
arr = (int *)malloc(n * sizeof(int));
for (int i = 0; i < n; i++) {
scanf("%d", &arr[i]);
}
srand(time(NULL));
inPlaceQuickSort(0, n - 1);
printArray(n);
free(arr);
return 0;
}
int chooseRandomPivotIdx(int l_idx, int r_idx) {
return rand() % (r_idx - l_idx + 1) + l_idx;
}
void inPlaceQuickSort(int l_idx, int r_idx) {
// base case: l_idx가 r_idx보다 크거나 같으면 종료
if (l_idx >= r_idx) return;
int pivotIdx = chooseRandomPivotIdx(l_idx, r_idx);
int l_PartitionEndIdx, r_PartitionStartIdx;
// 분할 - 피벗을 기준으로 왼쪽은 피벗보다 작고 오른쪽은 피벗보다 크다
inPlacePartition(l_idx, r_idx, pivotIdx, &l_PartitionEndIdx, &r_PartitionStartIdx);
// 왼쪽 부분 배열 정렬
inPlaceQuickSort(l_idx, l_PartitionEndIdx - 1);
// 오른쪽 부분 배열 정렬
inPlaceQuickSort(r_PartitionStartIdx + 1, r_idx);
}
void inPlacePartition(int l_idx, int r_idx, int pivotIdx, int* l_PartitionEndIdx, int* r_PartitionStartIdx) {
int pivot = arr[pivotIdx];
swap(&arr[pivotIdx], &arr[r_idx]); // 피벗을 배열의 오른쪽 끝으로 이동시켜 숨긴다
// i: 피벗보다 작은 값들이 모이는 위치
// cur: 현재 검사중인 위치
// j: 피벗보다 큰 값들이 모이는 위치
int i = l_idx, cur = l_idx, j = r_idx;
while (cur < j) {
if (arr[cur] < pivot) { // 피벗보다 작은 경우
swap(&arr[i], &arr[cur]);
i++;
}
else if (arr[cur] > pivot) { // 피벗보다 큰 경우
swap(&arr[cur], &arr[--j]);
continue; // cur을 증가시키지 않고 다음 반복에서 다시 검사
}
cur++;
}
swap(&arr[j], &arr[r_idx]); // 피벗을 제자리로 이동
// leftPartitionEnd와 rightPartitionStart를 업데이트
*l_PartitionEndIdx = i; // 피벗보다 작은 값들의 끝 인덱스 (피벗의 시작 인덱스)
*r_PartitionStartIdx = j; // 피벗의 시작 인덱스
}
void swap(int* ptr1, int* ptr2) {
int temp = *ptr1;
*ptr1 = *ptr2;
*ptr2 = temp;
}
void printArray(int n) {
for (int i = 0; i < n; i++) {
printf(" %d", arr[i]);
}
}
/*
3
4 9 1
8
73 65 48 31 29 20 8 3
5
2 3 3 1 5
*/
(참고)
https://www.youtube.com/watch?v=cWH49IKDIiI
방식이 살짝 다르기는 하지만 quickSort에서 partition함수를 이해하는 데에 이만한 영상이 없다.. 꼭 보도록 하자!
출처 및 참고: 알고리즘-원리와 응용(국형준교수님), Algorithm Design(Jon Kleinberg, Eva Tardos), Foundations of Algorithms using C++(Richard Neapolitan)
'Computer Science > 알고리즘' 카테고리의 다른 글
| [알고리즘] ep1-4+) O(n + klog(n))의 힙정렬 (1) | 2024.07.10 |
|---|---|
| [알고리즘] 정렬 알고리즘 선택 매뉴얼 (1) | 2024.07.07 |
| [알고리즘] ep1-5) 병합정렬(merge sort) (1) | 2024.07.05 |
| [알고리즘] ep1-4) 힙정렬(heap sort) (0) | 2024.07.04 |
| [알고리즘] ep1-3) 힙(heap) (0) | 2024.07.03 |


