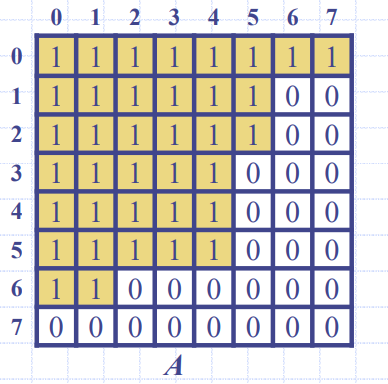
그림과 같은 비트행렬 A가 있다고 하자, 1을 카운트하는 방법에는 다양한 방법들이 존재한다
여기서 나는 2가지 방법을 얘기하려 한다
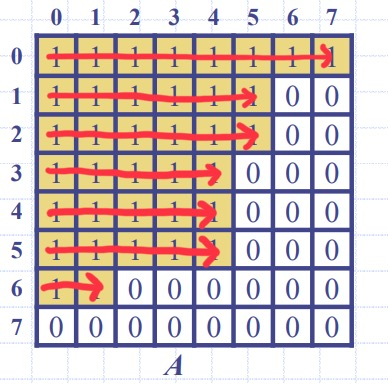
1. 가장 일반적인 방법으로 이중포문을 이용해 각 행마다 0이 나올 때까지 카운트를 하는 방법: O(n^2)
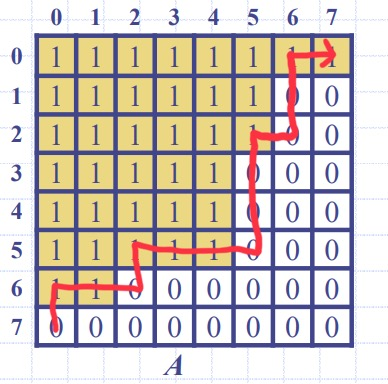
2. 제일 하단 좌측에서 시작해 우측 상단을 향해 지그재그 방식으로 올라오며 카운트를 하는 방법: O(n)
1번 방식은 시간복잡도가 O(n^2)이므로 n값이 커질수록 실행 시간은 제곱수로 증폭하게 된다
반면에, 2번 방식은 시간복잡도가 O(n)이므로 n값이 커질 수록 실행 시간은 그저 선형적으로 증가하게 된다
따라서 우리는 실행 시간의 측면에서 2번 방식이 압도적으로 더 좋은 것을 알 수가 있다
그렇기에 우리는 상황에 맞는 자료구조와 알고리즘을 설계할 수 있는 능력을 길러야 한다
(전체코드)
#include <stdio.h>
#include <stdlib.h>
int countOnesButSlow(int** A, int n); // O(n^2)
int countOnes(int** A, int n); // O(n) - 제일 하단 좌측에서부터 시작해 지그재그로 올라온다
int main(void) {
int n;
int** A;
scanf("%d", &n);
A = (int**)malloc(n * sizeof(int*)); // 2차원 배열 동적할당
for (int i = 0; i < n; i++) {
A[i] = (int*)malloc(n * sizeof(int));
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
scanf("%d", &A[i][j]);
}
}
printf("%d\n", countOnesButSlow(A, n));
printf("%d\n", countOnes(A, n));
for (int i = 0; i < n; i++) {
free(A[i]);
}
free(A);
return 0;
}
int countOnesButSlow(int** A, int n) { // O(n^2)
int row;
int cnt, cntSum;
row = 0, cnt = 0, cntSum = 0;
for (int i = 0; i < n; i++) {
cnt = 0;
while (A[i][cnt] == 1 && cnt < n) {
cnt++;
}
cntSum += cnt;
}
return cntSum;
}
int countOnes(int** A, int n) { // O(n) - 제일 하단 좌측에서부터 시작해 지그재그로 올라온다
int row, col;
int cnt;
row = n - 1, col = 0, cnt = 0;
while (col <= n && row >= 0) {
if (A[row][col] == 1) {
col++;
continue;
}
else if (A[row][col] == 0 || col == n) {
cnt += col;
row--;
}
}
return cnt;
}
/*
8
1 1 1 1 1 1 1 1
1 1 1 1 1 1 0 0
1 1 1 1 1 1 0 0
1 1 1 1 1 0 0 0
1 1 1 1 1 0 0 0
1 1 1 1 1 0 0 0
1 1 0 0 0 0 0 0
0 0 0 0 0 0 0 0
*/
참고 및 출처: 데이터 구조 원리와 응용(국형준교수님)
'Computer Science > 자료구조' 카테고리의 다른 글
| [자료구조] ep3-1) 단일연결리스트(Single Linked List) (2) | 2024.05.03 |
|---|---|
| [자료구조] ep2+) 하노이 탑 구현 (1) | 2024.04.07 |
| [자료구조] ep2) 재귀(Recursion) (0) | 2024.04.07 |
| [자료구조] ep1) 자료구조 기본 지식들 (1) | 2024.04.07 |
| [자료구조] ep0) 자료구조란? (0) | 2024.01.18 |



