ㅁ수식표기법: 이항연산을 표현하는 방법으로, 연산자와 피연산자의 위치를 어떻게 적는지에 따라 3가지로 나뉜다
1. 중위수식(infix expression): 연산자를 피연산자 사이에 배치
- 우리가 일반적으로 사용하는 수식
- 암묵적 우선순위(precedence)
- 우선순위는 괄호에 의해 무시
예시: (A+B)xC-(DxE)
2. 후위수식(postfix expression): 연산자를 피연산자 뒤에 배치 (컴파일러가 사용하는 방식)
- 역폴란드식(reverse Polish) 표기
- 우선순위 x
- 괄호 x
- 스택을 사용
예시: AB+CxDEx-
3. 전위수식(prefix expression): 연산자를 피연산자 앞에 배치
- 폴란드식(Polish) 표기
예시: -x+ABCxDE
문제1) 스택을 이용하여 입력 중위수식을 후위수식으로 변환 출력하는 프로그램을 작성하시오.
- 스택은 배열이나 연결리스트로 구현함.
- 수식의 피연산자는 영문자(대문자)로 나타내고, 각 수식의 최대길이는 100으로 함.
- 수식은 다음 표에 보인 우선순위를 가지는 연산자들을 포함함(숫자가 높을수록 우선순위가 높음).
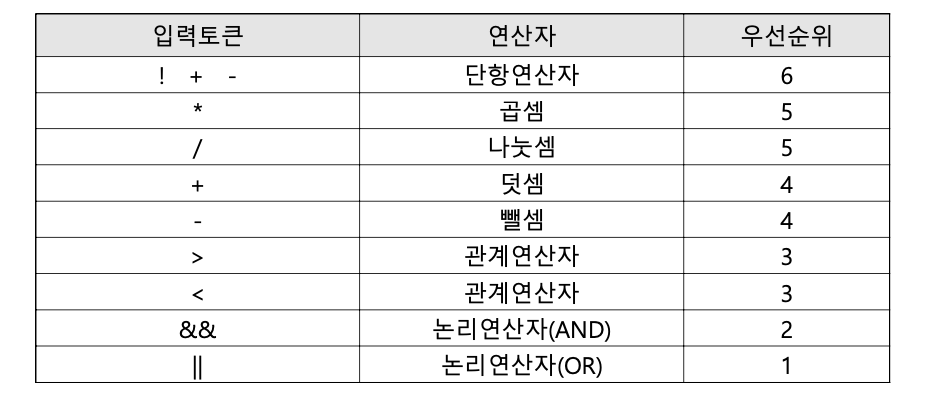
- 같은 우선순위를 갖는 이항연산자들은 왼쪽에서 오른쪽으로 계산(단항연산자는 반대 방향).
- 입출력에 대한 설명(다음 입출력 예시 참조)
- 1) 첫 번째 라인 : 수식의 개수
2) 두 번째 라인 : 한 개의 라인에 수식이 공백 없이 입력됨.

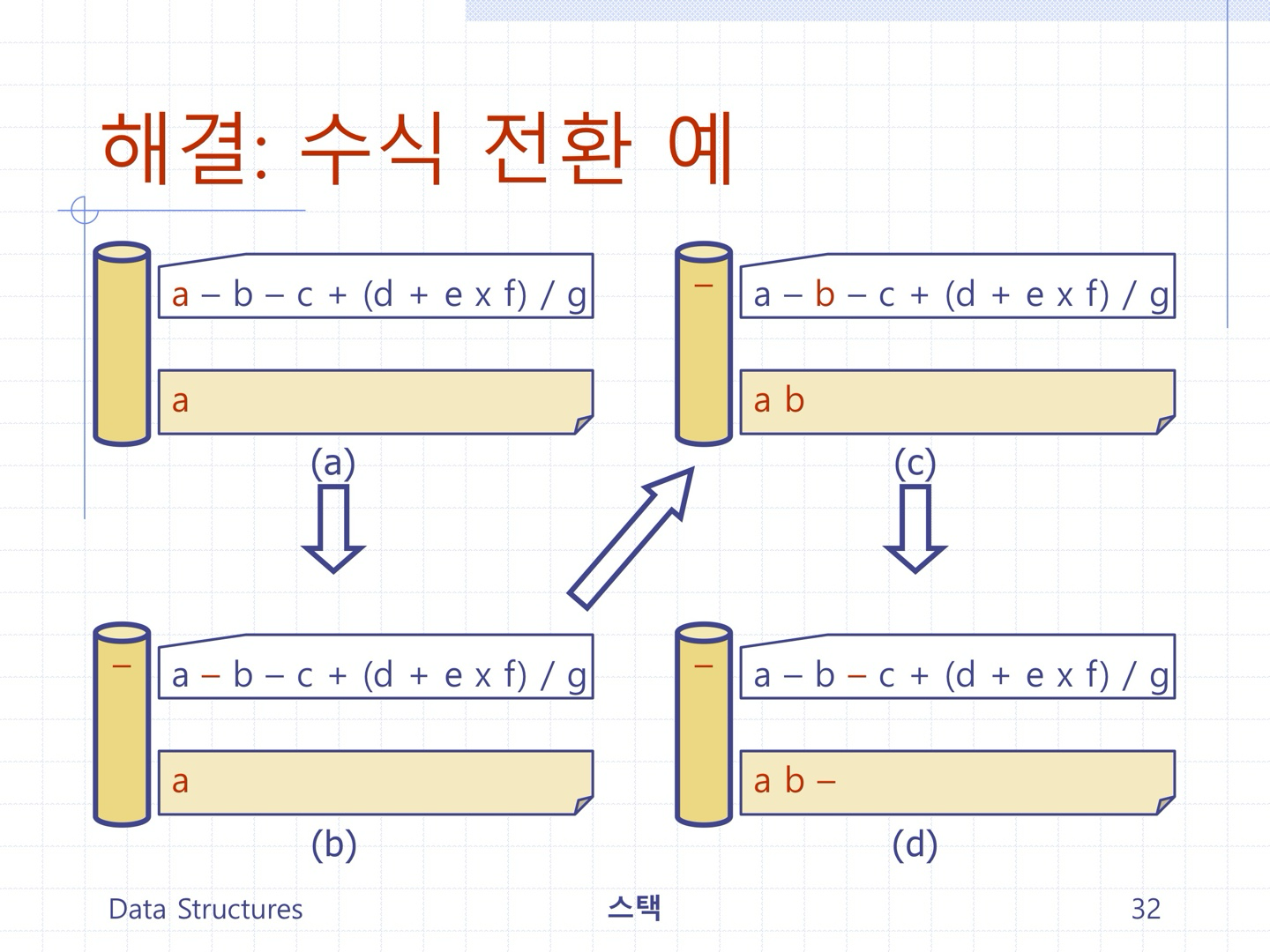
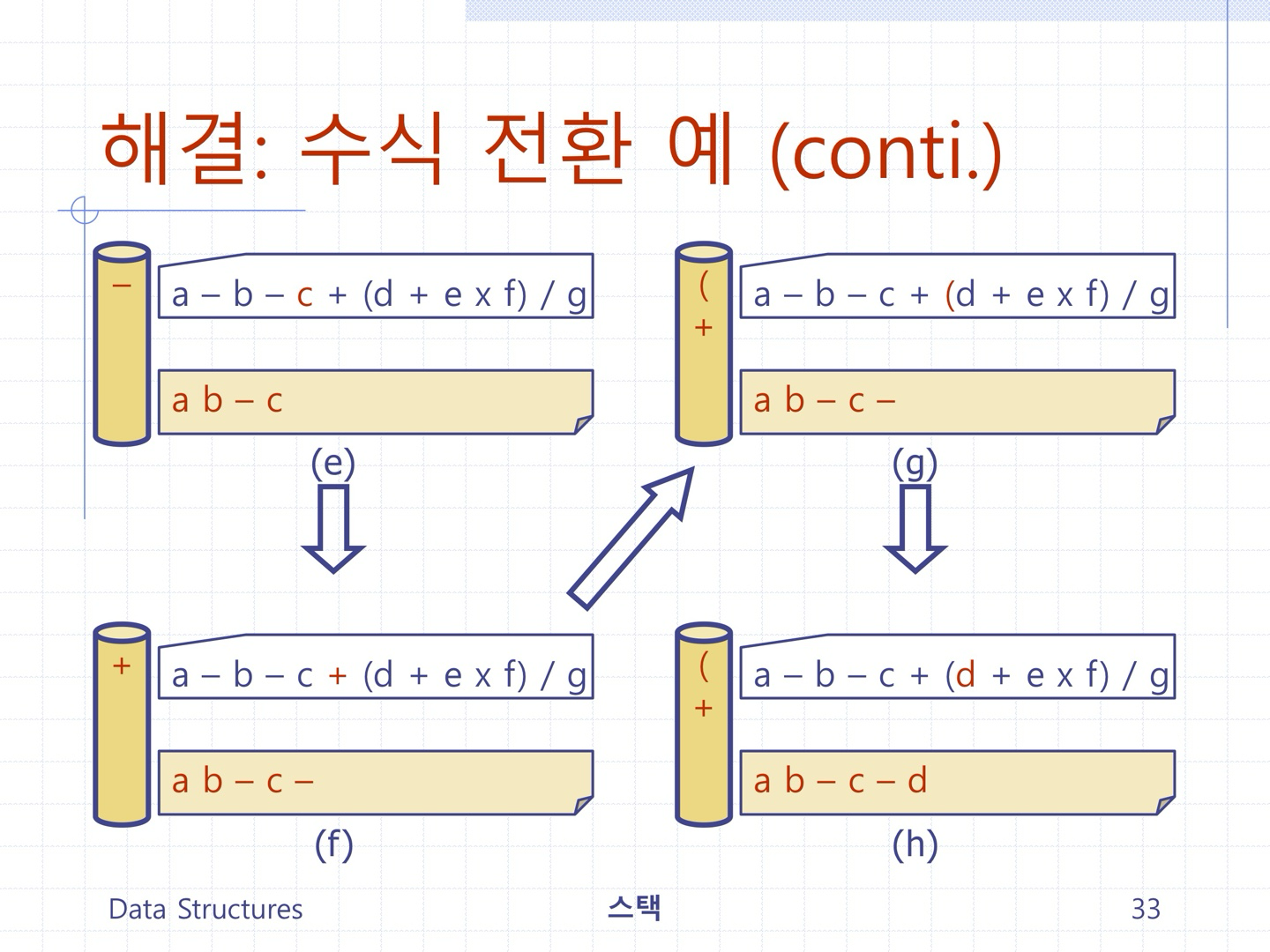
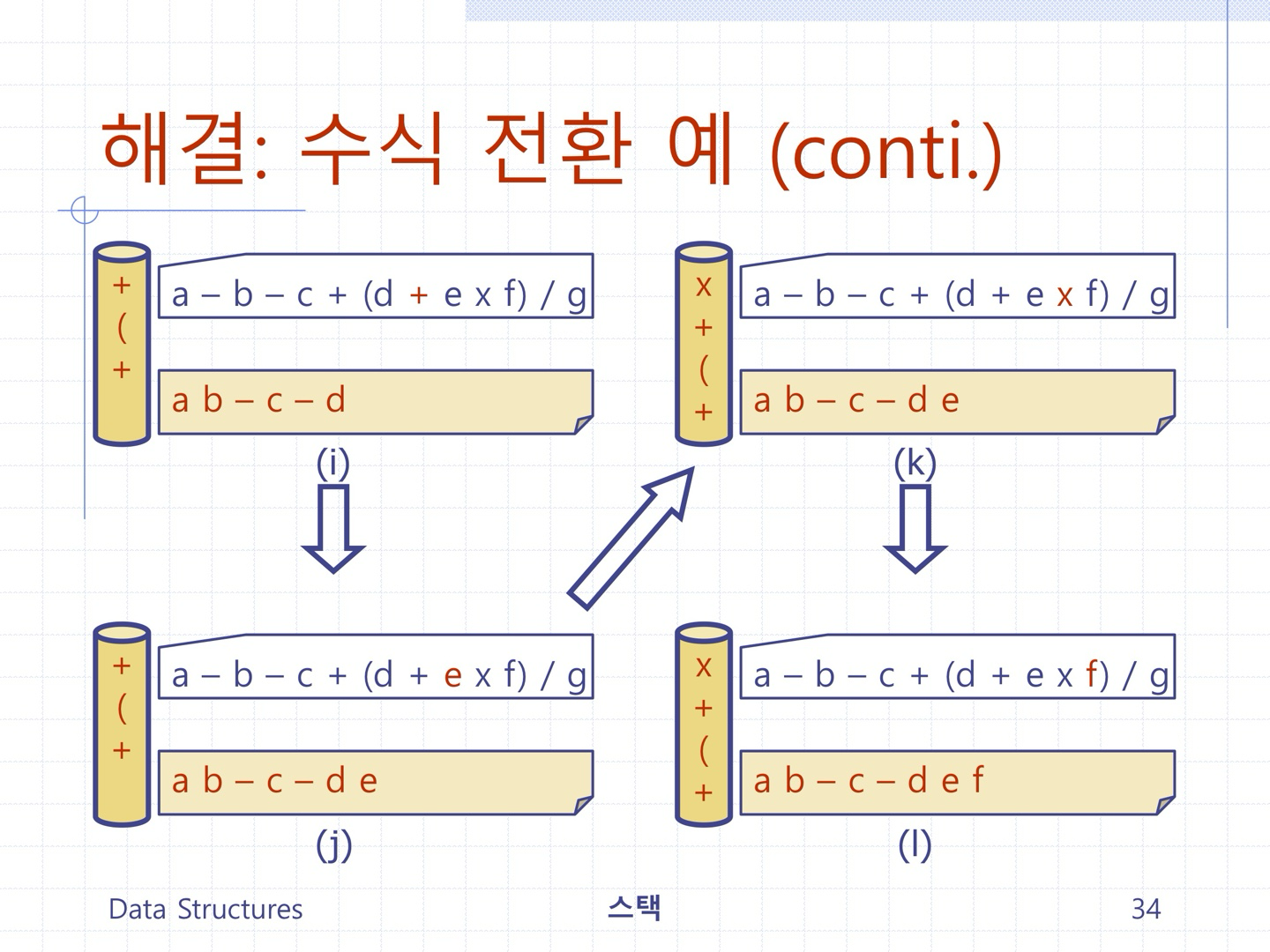

(전체코드)
// 스택에는 기호(연산자)가 들어간다
#include <stdio.h>
#include <stdlib.h>
#define MAX_SIZE 101
// 스택 구조체
typedef struct STACK {
char operator[MAX_SIZE];
int top;
} STACK;
int isEmpty(STACK* stack);
void push(STACK *stack, char operator);
char pop(STACK *stack);
char peek(STACK *stack);
void convert(char* str); // 중위수식을 후위수식으로 변환
int priority(char operator);
int isOperator(char c);
int main() {
int N;
char str[MAX_SIZE] = {0};
scanf("%d", &N);
for (int i = 0; i < N; i++) {
scanf("%s", str);
convert(str);
}
return 0;
}
int isEmpty(STACK* stack) {
return (stack->top == -1);
}
void push(STACK *stack, char operator) {
stack->operator[++(stack->top)] = operator;
}
char pop(STACK *stack) {
if (isEmpty(stack)) {
return 0;
}
return stack->operator[(stack->top)--];
}
char peek(STACK *stack) {
if (isEmpty(stack)) {
return 0;
}
return stack->operator[stack->top];
}
void convert(char* str) { // 중위수식을 후위수식으로 변환
STACK* stack = (STACK*)malloc(1 * sizeof(STACK));
stack->top = -1;
for (int i = 0; str[i] != '\0'; i++) {
if (str[i] >= 'A' && str[i] <= 'Z') { // 피연산자 case
printf("%c", str[i]);
}
else if (str[i] == '(') {
push(stack, str[i]); // 여는 괄호일 때 push
}
else if (str[i] == ')') {
while (peek(stack) != '(') {
printf("%c", pop(stack)); // 닫는 괄호일 때 '(' 전까지 모두 pop
}
pop(stack); // 여는 괄호 제거
}
else { // 기호(연산자) case
if (str[i] == '&' || str[i] == '|') { // 논리연산자의 경우 (&&, ||)
while (priority(str[i]) <= priority(peek(stack))) {
printf("%c", pop(stack)); // 현재 연산자보다 우선순위가 높은 기호(연산자)들을 출력
}
push(stack, str[i++]); // 현재 기호(연산자)를 스택에 추가
push(stack, str[i]); // 현재 기호(연산자)를 스택에 추가
continue;
}
else if (str[i] == '+' || str[i] == '-') { // 단항연산자 +, -의 경우
// start with + or -
// or such as *+ , /-, (+ ...
// or -ABC...
// but not )-
if (isOperator(str[i - 1]) && str[i - 1] != ')') {
push(stack, (str[i] == '+')? '@' : '#'); // +와 -를 @와 #으로 치환해서 push
continue;
}
else if (i == 0) {
push(stack, (str[i] == '+')? '@' : '#'); // +와 -를 @와 #으로 치환해서 push
continue;
}
}
// 그 외의 경우
while (priority(str[i]) <= priority(peek(stack))) { // 현재 연산자보다 우선순위가 높은 기호(연산자)들을 출력
if (peek(stack) == '@') {
pop(stack);
printf("%c", '+');
}
else if (peek(stack) == '#') {
pop(stack);
printf("%c", '-');
}
else {
printf("%c", pop(stack));
}
}
push(stack, str[i]); // 현재 기호(연산자)를 스택에 추가
}
}
// 스택에 남은 나머지 기호(연산자)들을 출력
while (!isEmpty(stack)) {
printf("%c", pop(stack));
}
printf("\n");
}
int priority(char operator) {
if (operator == '!' || operator == '@' || operator == '#') // 단항연산자의 경우
return 6;
else if (operator == '*' || operator == '/')
return 5;
else if (operator == '+' || operator == '-')
return 4;
else if (operator == '>' || operator == '<')
return 3;
else if (operator == '&')
return 2;
else if (operator == '|')
return 1;
else
return 0;
}
int isOperator(char c) {
return (c == '+'
|| c == '-'
|| c == '*'
|| c == '/'
|| c == '&'
|| c == '|'
|| c == '!'
|| c == '<'
|| c == '>'
|| c == '('
|| c == ')');
}
/*
5
A*B+C+(D+E)*F
A+B*C
A/B-C+D*E-F*G
A+(B*C+D)*E
A&&B||C||!(E>F)
AB*C+DE+F*+
ABC*+
AB/C-DE*+FG*-
ABC*D+E*+
AB&&C||EF>!||
*/
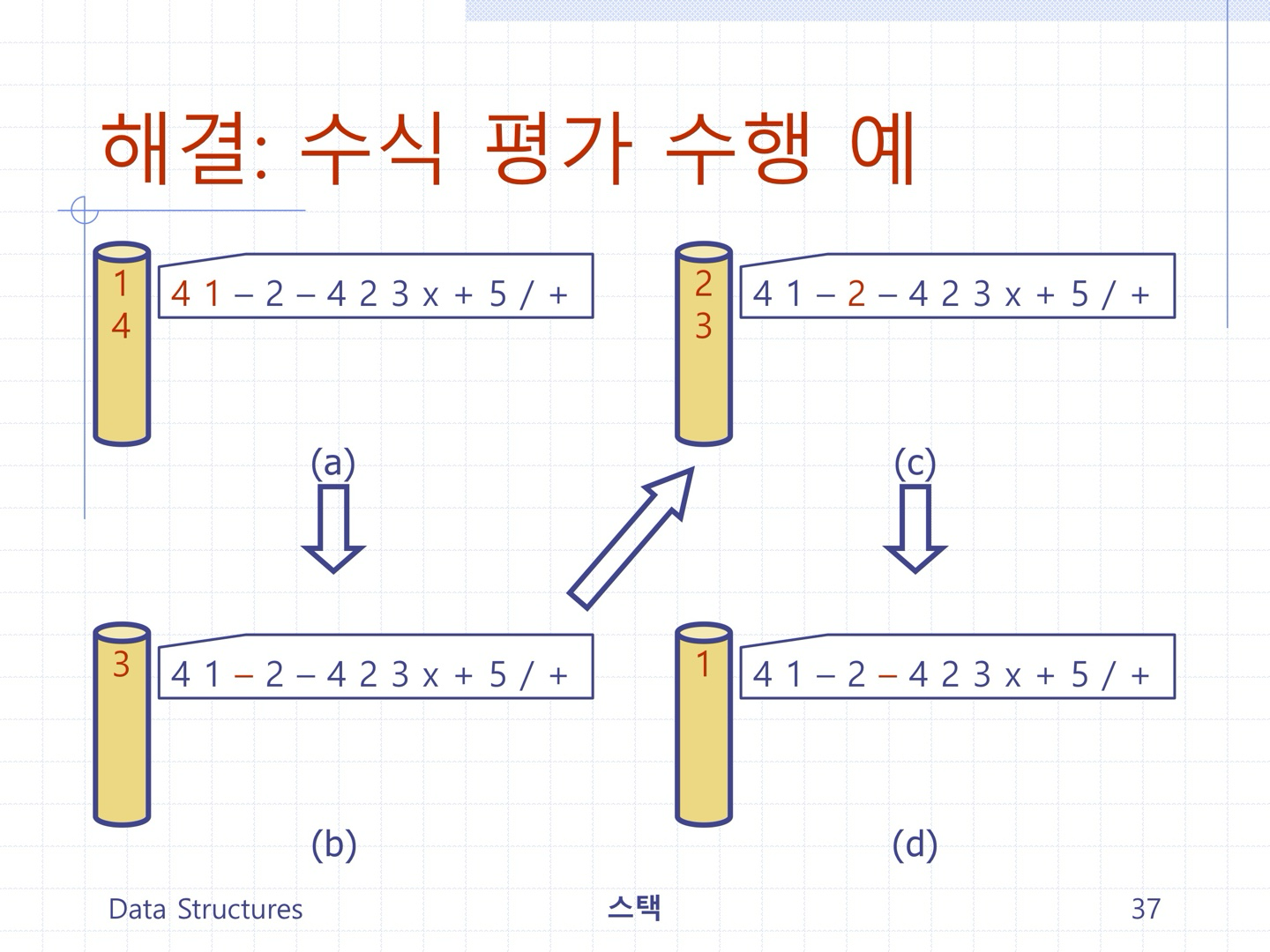
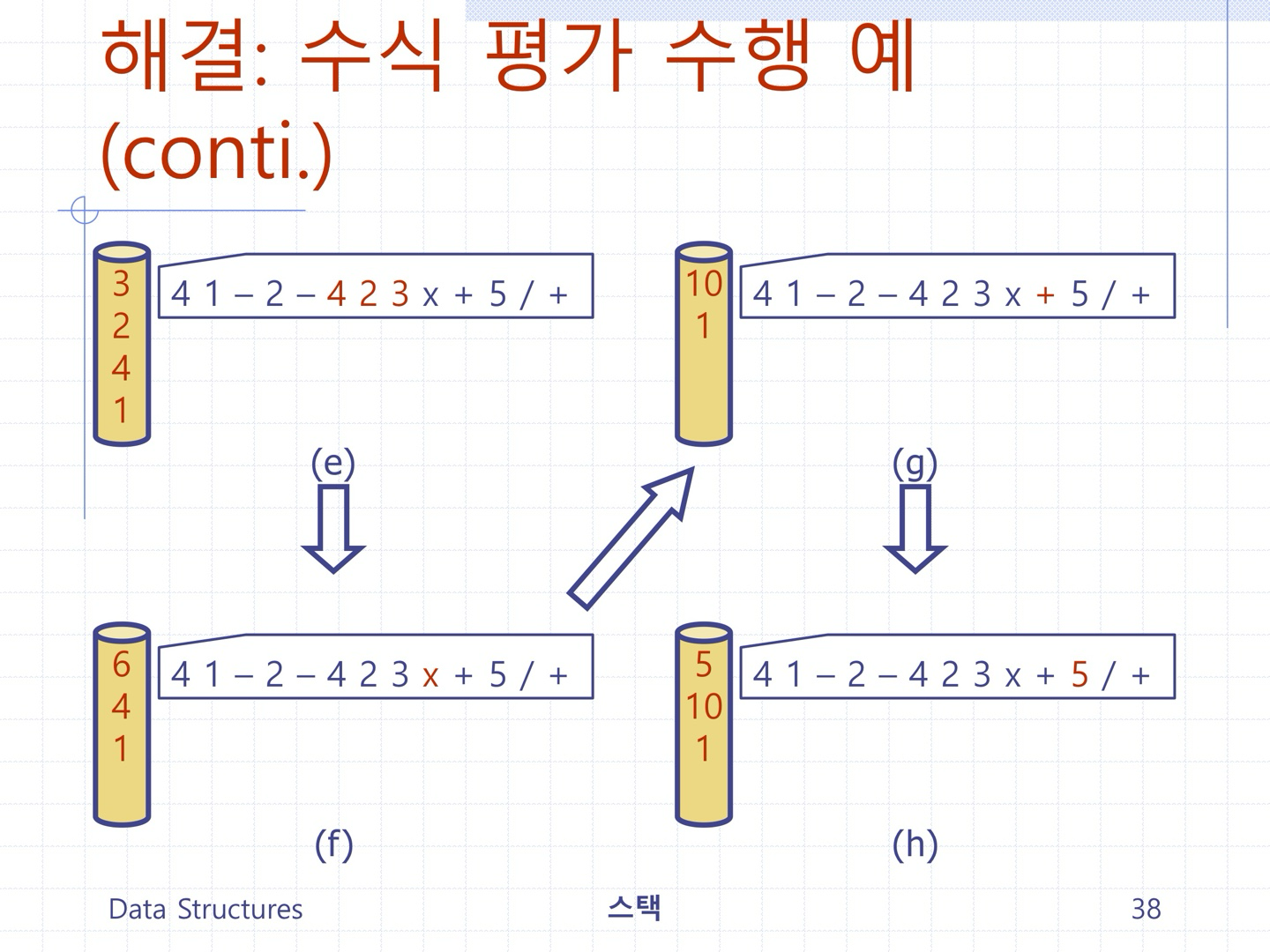
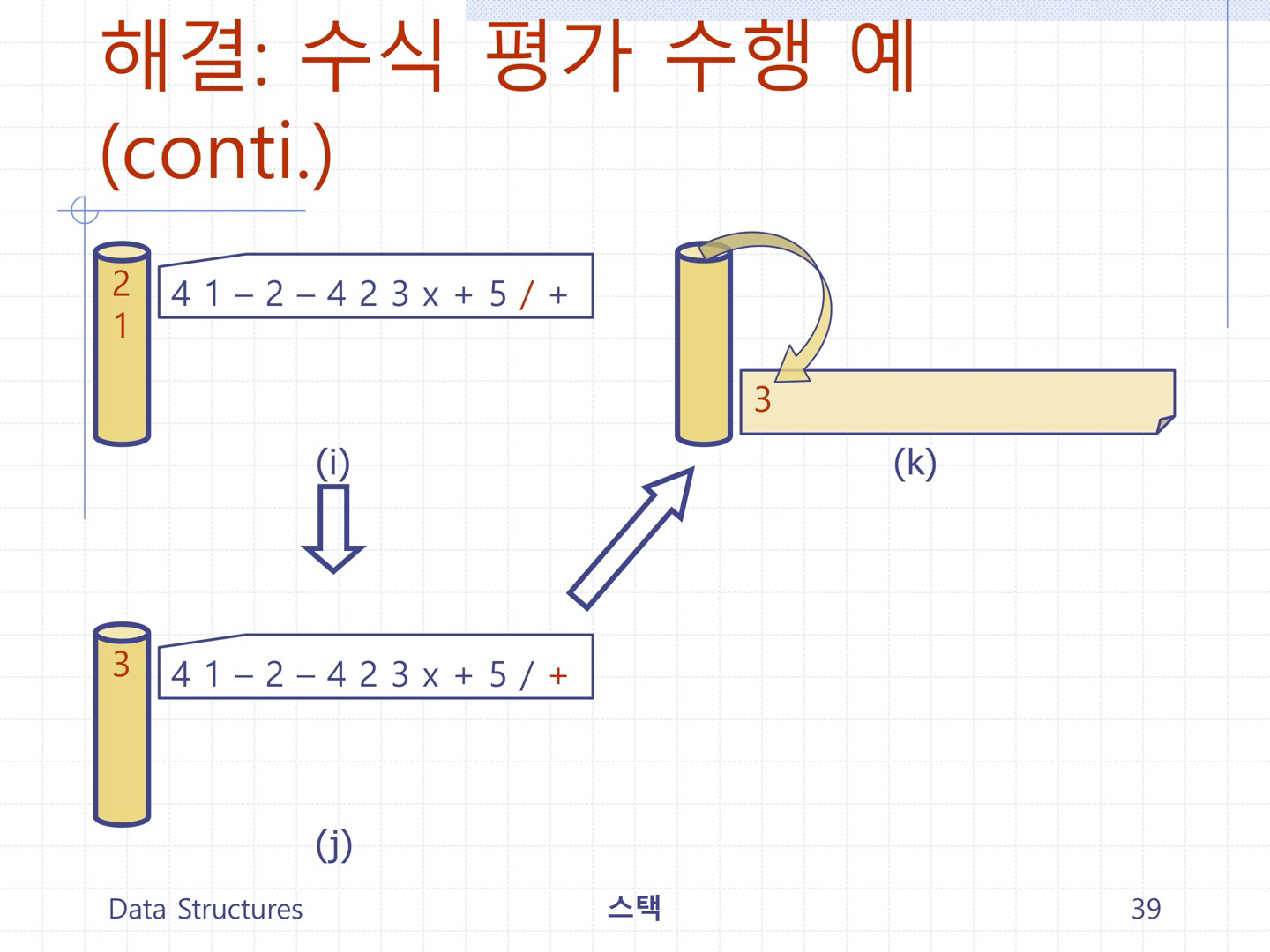
문제2) 스택을 이용하여 입력 후위수식을 평가한 값을 출력하는 프로그램을 작성하시오.
- 스택은 배열이나 연결리스트로 구현함.
- 수식의 피연산자는 0에서 9 사이의 정수고, 각 수식의 최대길이는 100으로 함.
- 수식의 연산자는 곱하기, 나누기, 더하기, 빼기로 구성되며, 모두 정수 연산을 수행한다. (즉, 나누기의 경우, 정수 몫 계산)
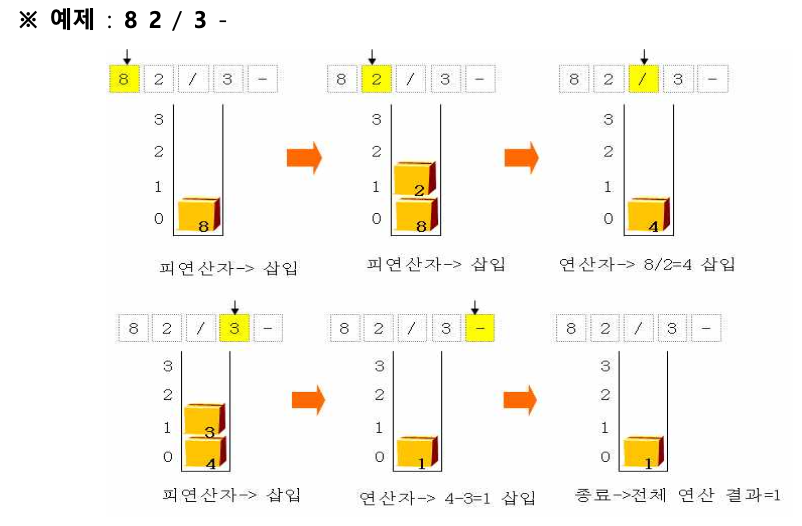
◦ 입출력에 대한 설명(다음 입출력 예시 참조)
1) 첫 번째 라인 : 수식의 개수
2) 두 번째 라인 : 한 개의 라인에 후위수식이 공백 없이 입력됨.

(전체코드)
#include <stdio.h>
#include <stdlib.h>
#define MAX_SIZE 101
// 스택 구조체
typedef struct STACK {
int n[MAX_SIZE];
int top;
} STACK;
void push(STACK* stack, int n);
int pop(STACK* stack);
int evaluate(char* str);
int main() {
int N;
char str[101] = {0};
scanf("%d", &N);
for (int i = 0; i < N; i++) {
scanf("%s", str);
printf("%d\n", evaluate(str));
}
return 0;
}
int isEmpty(STACK* stack) {
return (stack->top == -1);
}
void push(STACK* stack, int n) {
stack->n[++(stack->top)] = n;
}
int pop(STACK* stack) {
return stack->n[(stack->top)--];
}
int evaluate(char* str) {
STACK* stack = (STACK*)malloc(1 * sizeof(STACK));
stack->top = -1;
int op1, op2;
for (int i = 0; str[i] != '\0'; i++) {
if (str[i] == '*' || str[i] == '/' || str[i] == '+' || str[i] == '-') {
op2 = pop(stack);
op1 = pop(stack);
if (str[i] == '*') {
push(stack, op1 * op2);
}
else if (str[i] == '/') {
push(stack, op1 / op2);
}
else if (str[i] == '+') {
push(stack, op1 + op2);
}
else if (str[i] == '-') {
push(stack, op1 - op2);
}
}
else { // 숫자 case
push(stack, str[i] - '0');
}
}
int res = pop(stack);
free(stack);
return res;
}
/*
4
53*2+63+2*+
234*+
72/3-42*+21*-
923*1+2*+
*/
참고 및 출처: 데이터 구조 원리와 응용(국형준교수님)
'Computer Science > 자료구조' 카테고리의 다른 글
| [자료구조] ep6-1) 큐(Queue) (0) | 2024.06.08 |
|---|---|
| [자료구조] ep5+++) 시간복잡도를 고려한 스택 설계 (1) | 2024.06.08 |
| [자료구조] ep5+) 심볼 균형(스택을 이용한 괄호 쌍의 대칭성 검사) (0) | 2024.06.08 |
| [자료구조] ep5) 스택(Stack) (0) | 2024.06.07 |
| [자료구조] ep4+) 집합 ADT 활용문제들 (0) | 2024.05.03 |



